题目内容
已知函数![]() 。
。
(1)若函数![]() 是
是![]() 上的增函数,求实数
上的增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若不等式
时,若不等式![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)对于函数![]() 若存在区间
若存在区间![]() ,使
,使![]() 时,函数
时,函数![]() 的值域也是
的值域也是![]() ,则称
,则称![]() 是
是![]() 上的闭函数。若函数
上的闭函数。若函数![]() 是某区间上的闭函数,试探求
是某区间上的闭函数,试探求![]() 应满足的条件。
应满足的条件。
(1)![]() (2)
(2)![]() (3)
(3)![]()
解析:
(1) 当![]() 时,
时,![]()
设![]() 且
且![]() ,由
,由![]() 是
是![]() 上的增函数,则
上的增函数,则![]() 2分
2分
![]() 3分
3分
由![]() ,
,![]() 知
知![]() ,所以
,所以![]() ,即
,即![]() 5分
5分
(2)当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 6分
6分
因为![]() ,当
,当![]() 即
即![]() 时取等号, 8分
时取等号, 8分
![]() ,所以
,所以![]() 在
在![]() 上的最小值为
上的最小值为![]() 。则
。则![]() 10分
10分
(3)因为![]() 的定义域是
的定义域是![]() ,设
,设![]() 是区间
是区间![]() 上的闭函数,则
上的闭函数,则![]() 且
且![]() 11分
11分
①若![]()
当![]() 时,
时,![]() 是
是![]() 上的增函数,则
上的增函数,则![]() ,
,
所以方程![]() 在
在![]() 上有两不等实根,
上有两不等实根,
即![]() 在
在![]() 上有两不等实根,所以
上有两不等实根,所以
 ,即
,即![]() 且
且![]() 13分
13分
当![]() 时,
时,![]() 在
在![]() 上递减,则
上递减,则![]() ,即
,即
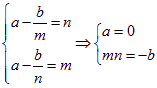 ,所以
,所以![]() 14分
14分
②若![]()
当![]() 时,
时,![]() 是
是![]() 上的减函数,所以
上的减函数,所以![]() ,即
,即
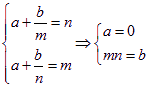 ,所以
,所以![]() 15分
15分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |