题目内容
设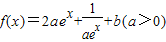 .
.(1)若f(0)=0,求实数b的取值范围;
(2)当b=0时,求f(x)在[0,+∞)上的最小值.
【答案】分析:(1)把f(0)=0,代入f(x)可以得出b关于a的表达式,再根据均值不等式,求出b的取值范围;
(2)b=0,可以求出f(x)的解析式,对f(x)进行分析,讨论2a2与1的大小,求出f(x)的单调区间,从而求出最小值;
解答:解:(1)∵f(0)=0,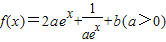
所以得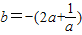 ,
,
由于a>0,
所以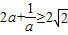 ,
,
于是b的取值范围是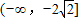
(2)当b=0时,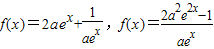 ,由于x≥0,所以ex≥1.
,由于x≥0,所以ex≥1.
①当2a2≥1即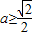 时,2a2e2x-1≥0,
时,2a2e2x-1≥0,
故f(x)≥0,f(x)在[0,+∞)上单调递增,
其最小值为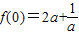
②当2a2<1即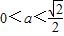 时,f(x)=0,得
时,f(x)=0,得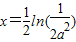 ,
,
且当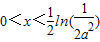 时,f(x)<0;当
时,f(x)<0;当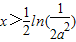 时,f(x)>0
时,f(x)>0
故f(x)在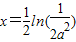 处取得极小值,由于极小值唯一,所以极小值就是最小值.
处取得极小值,由于极小值唯一,所以极小值就是最小值.
最小值为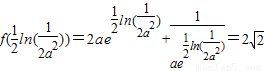
综上,当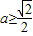 时,f(x)在[0,+∞)上最小值为
时,f(x)在[0,+∞)上最小值为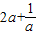 ;
;
当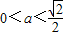 时,f(x)在[0,+∞)上的最小值为
时,f(x)在[0,+∞)上的最小值为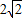
点评:此题主要考查函数值的代入,第二问求函数的单调区间,没有利用导数进行求解,直接进行讨论,会比较简单些!
(2)b=0,可以求出f(x)的解析式,对f(x)进行分析,讨论2a2与1的大小,求出f(x)的单调区间,从而求出最小值;
解答:解:(1)∵f(0)=0,
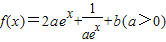
所以得
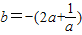 ,
,由于a>0,
所以
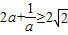 ,
,于是b的取值范围是
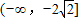
(2)当b=0时,
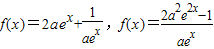 ,由于x≥0,所以ex≥1.
,由于x≥0,所以ex≥1.①当2a2≥1即
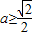 时,2a2e2x-1≥0,
时,2a2e2x-1≥0,故f(x)≥0,f(x)在[0,+∞)上单调递增,
其最小值为
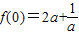
②当2a2<1即
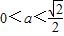 时,f(x)=0,得
时,f(x)=0,得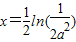 ,
,且当
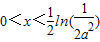 时,f(x)<0;当
时,f(x)<0;当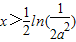 时,f(x)>0
时,f(x)>0故f(x)在
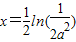 处取得极小值,由于极小值唯一,所以极小值就是最小值.
处取得极小值,由于极小值唯一,所以极小值就是最小值.最小值为
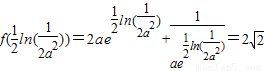
综上,当
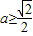 时,f(x)在[0,+∞)上最小值为
时,f(x)在[0,+∞)上最小值为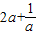 ;
;当
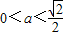 时,f(x)在[0,+∞)上的最小值为
时,f(x)在[0,+∞)上的最小值为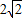
点评:此题主要考查函数值的代入,第二问求函数的单调区间,没有利用导数进行求解,直接进行讨论,会比较简单些!

练习册系列答案
相关题目
 .
.