题目内容
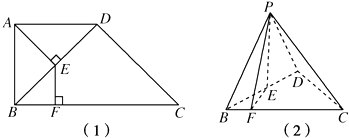 如图(1),四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起,记折起后点A的位置为P,且使平面PBD⊥平面BCD,如图(2).
如图(1),四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起,记折起后点A的位置为P,且使平面PBD⊥平面BCD,如图(2).(I)求证:平面PBC⊥平面PDC;
(II)在折叠前的四边形ABCD中,作AE⊥BD于E,过E作EF⊥BC于F,求折起后的图形中∠PFE的正切值.
分析:(I)利用折叠前四边形ABCD中的性质与数量关系,可证BD⊥CD,再利用折叠后BCD平面PBD⊥平面,可证CD⊥平面PBD,从而证明CD⊥PB,
再证明PB⊥平面PDC,然后利用线面垂直证明面面垂直.
(II)利用(1)证明PE⊥平面BCD,从而证明PE⊥EF,再通过解Rt△BEF,求EF,然后解Rt△PEF求tan∠PFE的值.
再证明PB⊥平面PDC,然后利用线面垂直证明面面垂直.
(II)利用(1)证明PE⊥平面BCD,从而证明PE⊥EF,再通过解Rt△BEF,求EF,然后解Rt△PEF求tan∠PFE的值.
解答: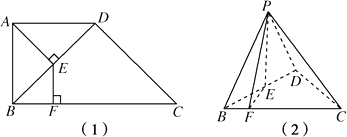 解:(I)证明:折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,∴△ABD为等腰直角三角形.
解:(I)证明:折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,∴△ABD为等腰直角三角形.
又∵∠BCD=45°,∠DBC=45°,∴∠BDC=90°.
折叠后,∵平面BCD⊥平面PBD,CD⊥BD,
∴CD⊥平面PBD.
又∵PB?平面PBD,∴CD⊥PB.
又PB⊥PD,PD∩CD=D,
∴PB⊥平面PDC.又PB?平面PBC,
∴平面PBC⊥平面PDC.
(II)∵AE⊥BD,EF⊥BC,折叠后的位置关系不变,∴PE⊥BD.
又平面PBD⊥平面BCD,∴PE⊥平面BCD,∴PE⊥EF.
设AB=AD=a,则BD=
a,∴PE=
a=BE.
在Rt△BEF中,EF=BE•sin45°=
a×
=
a.
在Rt△PEF中,tan∠PFE=
=
=
.
 解:(I)证明:折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,∴△ABD为等腰直角三角形.
解:(I)证明:折叠前,在四边形ABCD中,AD∥BC,AD=AB,∠BAD=90°,∴△ABD为等腰直角三角形.又∵∠BCD=45°,∠DBC=45°,∴∠BDC=90°.
折叠后,∵平面BCD⊥平面PBD,CD⊥BD,
∴CD⊥平面PBD.
又∵PB?平面PBD,∴CD⊥PB.
又PB⊥PD,PD∩CD=D,
∴PB⊥平面PDC.又PB?平面PBC,
∴平面PBC⊥平面PDC.
(II)∵AE⊥BD,EF⊥BC,折叠后的位置关系不变,∴PE⊥BD.
又平面PBD⊥平面BCD,∴PE⊥平面BCD,∴PE⊥EF.
设AB=AD=a,则BD=
| 2 |
| ||
| 2 |
在Rt△BEF中,EF=BE•sin45°=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
在Rt△PEF中,tan∠PFE=
| PE |
| EF |
| ||||
|
| 2 |
点评:本题通过折叠性问题,考查了面面垂直的性质,面面垂直的判定,考查了线面垂直的性质与判定,综合性强,关键是利用好直线与平面,平面与平面垂直关系的转化.

练习册系列答案
相关题目
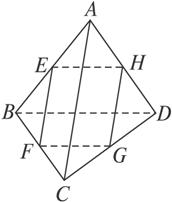
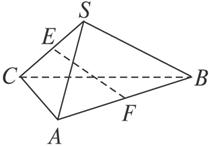
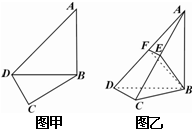 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.