题目内容
(2012•河南模拟)选修4-4:坐标系与参数方程
在直角坐标系xoy中,圆C的参数方程为
(θ为参数r>0)以O为极点,x轴的非负半轴为极轴,并取相同的长度单位建立极坐标系,直线l的极坐标方程ρsin(θ+
)=
.
(I)求圆心的极坐标.
(II)若圆C上点到直线l的最大距离为3,求r的值.
在直角坐标系xoy中,圆C的参数方程为
|
| π |
| 4 |
| ||
| 2 |
(I)求圆心的极坐标.
(II)若圆C上点到直线l的最大距离为3,求r的值.
分析:(Ⅰ)将圆的参数方程转化为普通方程,可求得圆心坐标,ρ与极角;
(Ⅱ)利用点到直线间的距离公式可求得圆心到直线l的距离,由圆C上点到直线l的最大距离dmax等于圆心C到l距离和半径之和即可求得r.
(Ⅱ)利用点到直线间的距离公式可求得圆心到直线l的距离,由圆C上点到直线l的最大距离dmax等于圆心C到l距离和半径之和即可求得r.
解答:解:(I)圆的直角坐标方程:(x+
)2+(y+
)2=r2+(y+
)2=1,
圆心坐标为C(-
,-
),ρ=
=1,
∴圆心C在第三象限,θ=
,
∴圆心极坐标为(1,
);
(II)∵圆C上点到直线l的最大距离dmax等于圆心C到l距离和半径之和,
l的直角坐标方程为:x+y-1=0,
∴dmax=
+r=3,
∴r=2-
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
圆心坐标为C(-
| ||
| 2 |
| ||
| 2 |
(-
|
∴圆心C在第三象限,θ=
| 5π |
| 4 |
∴圆心极坐标为(1,
| 5π |
| 4 |
(II)∵圆C上点到直线l的最大距离dmax等于圆心C到l距离和半径之和,
l的直角坐标方程为:x+y-1=0,
∴dmax=
|-
| ||||||||
|
∴r=2-
| ||
| 2 |
点评:本题考查圆的参数方程,着重考察圆的参数方程化普通方程的应用,考查极坐标方程与普通方程的转化,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
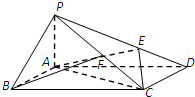 (2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.
(2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.