题目内容
已知椭圆的焦点是F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等差中项.(1)求椭圆的方程;
(2)若点P在第三象限,且∠PF1F2=120°,求tan∠F1PF2.
解:(1)由题设2|F1F2|=|PF1|+|PF2|,
∴2a=4,又2c=2,∴b=![]() .
.
∴椭圆的方程为![]() .
.
(2)设∠F1PF2=θ,则∠PF2F1=60°-θ.
由正弦定理得![]()
![]()
![]() .
.
由等比定理得![]()
![]() .
.
∴![]()
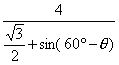 .
.
整理得5sinθ=![]() (1+cosθ).
(1+cosθ).
∴![]() .
.
故tan![]() =
=![]() ,tan∠F1PF2=tanθ=
,tan∠F1PF2=tanθ=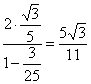 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知椭圆的焦点是F1,F2,P是椭圆上的一个动点,如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是( )
| A、椭圆 | B、双曲线的一支 | C、抛物线 | D、圆 |