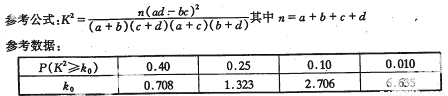题目内容
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
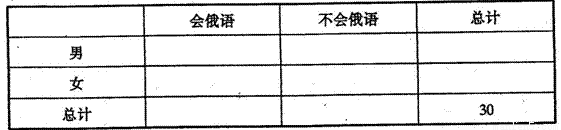
(I)根据以上数据完成以下2×2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
参考公式:K2=
其中n=a+b+c+d
参考数据:
(II)若从会俄语的记者中随机抽取3人成立一个小组,则小组中既有男又有女的概率是多少?
(III)若从14名女记者中随机抽取2人担任翻译工作,记会俄语的人数为ξ,求ξ的期望.
(I)根据以上数据完成以下2×2列联表:
| 会俄语 | 不会俄语 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 30 |
参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
(III)若从14名女记者中随机抽取2人担任翻译工作,记会俄语的人数为ξ,求ξ的期望.
(本题满分12分)
(Ⅰ)如下表:
…(2分)
假设:是否会俄语与性别无关.
由已知数据可求得K2=
≈1.1575<2.706
所以在犯错的概率不超过0.10的前提下不能判断会俄语与性别有关;…(5分)
(Ⅱ)从会俄语的记者中随机抽取3人成立一个小组,有
种选法,
小组中既有男又有女的选法有
+
种选法,
∴小组中既有男又有女的概率P=
=
; …(8分)
(Ⅲ)会俄语的人数ξ的取值分别为0,1,2.
其概率分别为P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,…(10分)
所以ξ的分布列为:
Eξ=0×
+1×
+2×
=
.…(12分)
(Ⅰ)如下表:
| 会俄语 | 不会俄语 | 总计 | |
| 男 | 10 | 6 | 16 |
| 女 | 6 | 8 | 14 |
| 总计 | 16 | 14 | 30 |
假设:是否会俄语与性别无关.
由已知数据可求得K2=
| 30×(10×8-6×6)2 |
| (10+6)(6+8)(10+6)(6+8) |
所以在犯错的概率不超过0.10的前提下不能判断会俄语与性别有关;…(5分)
(Ⅱ)从会俄语的记者中随机抽取3人成立一个小组,有
| C | 316 |
小组中既有男又有女的选法有
| 16 |
| C | 26 |
| C | 110 |
∴小组中既有男又有女的概率P=
| ||||||||
|
| 3 |
| 4 |
(Ⅲ)会俄语的人数ξ的取值分别为0,1,2.
其概率分别为P(ξ=0)=
| ||
|
| 28 |
| 91 |
P(ξ=1)=
| ||||
|
| 48 |
| 91 |
P(ξ=2)=
| ||
|
| 15 |
| 91 |
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 28 |
| 91 |
| 48 |
| 91 |
| 15 |
| 91 |
| 78 |
| 91 |

练习册系列答案
相关题目