题目内容
函数的导数为0的点称为函数的驻点,若点(1,1)为函数f(x)的驻点,则称f(x)具有“1-1驻点性”.
(1)设函数f(x)=-x+2
+alnx,其中a≠0.
①求证:函数f(x)不具有“1-1驻点性”
②求函数f(x)的单调区间
(2)已知函数g(x)=bx3+3x2+cx+2具有“1-1驻点性”,给定x1,x2∈R,x1<x2,设λ为实数,且λ≠-1,α=
,β=
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范围.
(1)设函数f(x)=-x+2
| x |
①求证:函数f(x)不具有“1-1驻点性”
②求函数f(x)的单调区间
(2)已知函数g(x)=bx3+3x2+cx+2具有“1-1驻点性”,给定x1,x2∈R,x1<x2,设λ为实数,且λ≠-1,α=
| x1+λx2 |
| 1+λ |
| x2+λx1 |
| 1+λ |
分析:(1)①对函数f(x)=-x+2
+alnx求导,验证f′(1)≠0即可说明函数f(x)不具有“1-1驻点性”;②根据导数的符号和函数单调性的关系,即f′(x)>0时不等式解集就是函数的单调递增区间,f′(x)<0时不等式解集就是函数的单调递减区间,注意对参数a的讨论;
(2)由题设知,函数g(x)得导数g′(x)=g′(x)=3bx2+6x+c,根据g(x)具有“1-1驻点性,求出b,c的值,从而g(x)在R上单调递减,分①λ≥0②-1<λ<0③λ<-1三种情况讨论求解λ得范围即可
| x |
(2)由题设知,函数g(x)得导数g′(x)=g′(x)=3bx2+6x+c,根据g(x)具有“1-1驻点性,求出b,c的值,从而g(x)在R上单调递减,分①λ≥0②-1<λ<0③λ<-1三种情况讨论求解λ得范围即可
解答:解:(1)①f′(x)=-1+
+
∵f′(1)=-1+1+a≠0,
∴函数f(x)不具有“1-1驻点性”.
②由f′(x)=
=
(ⅰ)当a+
<0,即a<-
时,f′(x)<0.∴f(x)是(0,+∞)上的减函数;
(ⅱ)当a+
=0,即a=-
时,显然f′(x)≤0.∴f(x)是(0,+∞)上的减函数
(ⅲ)当a+
>0,即a>-
时,由f′(x)=0得
=
±
当-
<a<0时,
-
>0
∴x∈(0,a+
-
)时,f′(x)<0;
x∈( a+
-
,a+
+
)时,f′(x)>0; x∈(a+
+
,+∞)时,f′(x)<0;
当a>0时,
-
<0
∴x∈(0,a+
+
)时,f′(x)>0; x∈( a+
+
,+∞)时,f′(x)<0;
综上所述:当a≤-
时,函数f(x)的单调递减区间为(0,+∞);
当-
<a<0时,函数f(x)的单调递减区间为(0,a+
-
)和( a+
+
,+∞),
函数f(x)的单调递增区间为( a+
-
,a+
+
);
当a>0时,函数f(x)的单调递增区间为(0,a+
+
),
函数f(x)的单调递减区间为( a+
+
,+∞)
(Ⅱ)由题设得:g′(x)=3bx2+6x+c,
∵g(x)具有“1-1驻点性”∴g(1)=1且g′(1)=0
即
解得
∴g′(x)=-3x2+6x-3=-3(x-1)2≤0,故g(x)在定义域R上单调递减.
①当λ≥0时,α=
≥
=x1,α=
<
=x2,即α∈[x1,x2),同理β∈(x1,x2]
由g(x)的单调性可知:g(α),g(β)∈[g(x2),g(x1)]
∴|g(α)-g(β)|≤|g(x1)-g(x2)|与题设|g(α)-g(β)|>|g(x1)-g(x2)|不符.
②当-1<λ<0时,α=
<
=x1,β=
>
=x2
即α<x1<x2<β∴g(β)<g(x2)<g(x1)<g(α)
∴|g(α)-g(β)|>|g(x1)-g(x2)|,符合题设
③当λ<-1时,α=
>
=x2,β=
<
=x1,即β<x1<x2<α
∴g(α)<g(x2)<g(x1)<g(β)
∴|g(α)-g(β)|>|g(x1)-g(x2)|也符合题设
由此,综合①②③得所求的λ的取值范围是λ<0且λ≠-1
| 1 | ||
|
| a |
| x |
∵f′(1)=-1+1+a≠0,
∴函数f(x)不具有“1-1驻点性”.
②由f′(x)=
-x+
| ||
| x |
-(
| ||||||
| x |
(ⅰ)当a+
| 1 |
| 4 |
| 1 |
| 4 |
(ⅱ)当a+
| 1 |
| 4 |
| 1 |
| 4 |
(ⅲ)当a+
| 1 |
| 4 |
| 1 |
| 4 |
| x |
| 1 |
| 2 |
a+
|
当-
| 1 |
| 4 |
| 1 |
| 2 |
a+
|
∴x∈(0,a+
| 1 |
| 2 |
a+
|
x∈( a+
| 1 |
| 2 |
a+
|
| 1 |
| 2 |
a+
|
| 1 |
| 2 |
a+
|
当a>0时,
| 1 |
| 2 |
a+
|
∴x∈(0,a+
| 1 |
| 2 |
a+
|
| 1 |
| 2 |
a+
|
综上所述:当a≤-
| 1 |
| 4 |
当-
| 1 |
| 4 |
| 1 |
| 2 |
a+
|
| 1 |
| 2 |
a+
|
函数f(x)的单调递增区间为( a+
| 1 |
| 2 |
a+
|
| 1 |
| 2 |
a+
|
当a>0时,函数f(x)的单调递增区间为(0,a+
| 1 |
| 2 |
a+
|
函数f(x)的单调递减区间为( a+
| 1 |
| 2 |
a+
|
(Ⅱ)由题设得:g′(x)=3bx2+6x+c,
∵g(x)具有“1-1驻点性”∴g(1)=1且g′(1)=0
即
|
|
∴g′(x)=-3x2+6x-3=-3(x-1)2≤0,故g(x)在定义域R上单调递减.
①当λ≥0时,α=
| x1+λx2 |
| 1+λ |
| x1+λx1 |
| 1+λ |
| x1+λx2 |
| 1+λ |
| x2+λx2 |
| 1+λ |
由g(x)的单调性可知:g(α),g(β)∈[g(x2),g(x1)]
∴|g(α)-g(β)|≤|g(x1)-g(x2)|与题设|g(α)-g(β)|>|g(x1)-g(x2)|不符.
②当-1<λ<0时,α=
| x1+λx2 |
| 1+λ |
| x1+λx1 |
| 1+λ |
| x2+λx1 |
| 1+λ |
| x2+λx2 |
| 1+λ |
即α<x1<x2<β∴g(β)<g(x2)<g(x1)<g(α)
∴|g(α)-g(β)|>|g(x1)-g(x2)|,符合题设
③当λ<-1时,α=
| x1+λx2 |
| 1+λ |
| x2+λx2 |
| 1+λ |
| x2+λx1 |
| 1+λ |
| x1+λx1 |
| 1+λ |
∴g(α)<g(x2)<g(x1)<g(β)
∴|g(α)-g(β)|>|g(x1)-g(x2)|也符合题设
由此,综合①②③得所求的λ的取值范围是λ<0且λ≠-1
点评:本题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力,属难题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 +alnx,其中a≠0.
+alnx,其中a≠0.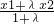 ,β=
,β=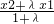 ,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范围.
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范围. +alnx,其中a≠0.
+alnx,其中a≠0. ,β=
,β= ,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范围.
,若|g(α)-g(β)|>|g(x1)-g(x2)|,求λ的取值范围.