题目内容
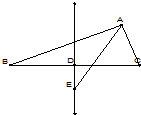
 如图,在∠AOB的两边上分别为A1,A2,A3,A4,B1,B2,B3,B4,B5共9个点,连接线段AiBj(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有
如图,在∠AOB的两边上分别为A1,A2,A3,A4,B1,B2,B3,B4,B5共9个点,连接线段AiBj(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有60
60
对“和睦线”.分析:本题是一个计数原理的实际应用,在∠AOB的两边各取两点Ai,Aj,(i<j)和Bj,Bp,(j<q),四边形AiAPBqBj中,恰有一个“和睦线对”(AiBj和APBq),在AO上取2点有C52种方法,在BO中取2点有C42种方法,相乘得到结果.
解答:解:由题意知本题是一个计数原理的实际应用,
在∠AOB的两边各取两点Ai,Aj,(i<j)和Bj,Bp,(j<q),
易见四边形AiAPBqBj中,恰有一个“和睦线对”(AiBj和APBq),
而在AO上取2点有C52=10种方法,
在BO中取2点有C42=6种方法,
图中共有10×6=60个“和睦线”.
故答案为:60.
在∠AOB的两边各取两点Ai,Aj,(i<j)和Bj,Bp,(j<q),
易见四边形AiAPBqBj中,恰有一个“和睦线对”(AiBj和APBq),
而在AO上取2点有C52=10种方法,
在BO中取2点有C42=6种方法,
图中共有10×6=60个“和睦线”.
故答案为:60.
点评:本题考查的是排列组合中的乘法原理,本题解题的关键是看出完成一件事所有的步骤和方法数,第一步有m种不同方法,第二步有n种不同方法,则完成这件一共有m×n种不同方法.

练习册系列答案
相关题目
 如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连接线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有( )对“和睦线”
如图,在∠AOB的两边上分别为A1、A2、A3、A4和B1、B2、B3、B4、B5共9个点,连接线段AiBi(1≤i≤4,1≤j≤5),如果其中两条线段不相交,则称之为一对“和睦线”,则图中共有( )对“和睦线”