题目内容
已知两点O(0,0),A(1,0),直线l:x-2y+1=0,P为直线l上一点.则|PO|+|PA|最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:求点O关于直线l的对称点B的坐标,根据P在直线AB上时,|PO|+|PA|最小,且最小值为|AB|,求解.
解答: 解:设O(0,0)关于直线l的对称点为B(a,b),
解:设O(0,0)关于直线l的对称点为B(a,b),
则
⇒
,∴B(-
,
),
当点P在直线AB上时,|PO|+|PA|最小,且最小值为|AB|=
=
.
故选B.
 解:设O(0,0)关于直线l的对称点为B(a,b),
解:设O(0,0)关于直线l的对称点为B(a,b),则
|
|
| 2 |
| 5 |
| 4 |
| 5 |
当点P在直线AB上时,|PO|+|PA|最小,且最小值为|AB|=
|
| ||
| 5 |
故选B.
点评:本题考查了点关于直线的对称点的求法,体现了数形结合思想.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知两点O(0,0),Q(a,b),点P1是线段OQ的中点,点P2是线段QP1的中点,P3是线段P1P2的中点,┅,Pn+2是线段PnPn+1的中点,则点Pn的极限位置应是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 在极坐标系中,已知两点O(0,0),B(2
在极坐标系中,已知两点O(0,0),B(2 ,
,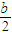 )
) )
) )
) )
)