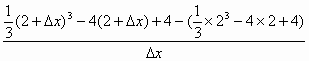Question

已知点M(0，－1)、F(0，1)，过点M的直线l与曲线y＝x³－4x＋4在x＝2处的切线平行．

(1)求直线l的方程；

(2)求以点F为焦点，l为准线的抛物线C的方程．

Answer 1

答案：
解析：

解：(1)因为(2) 　　＝ 　　＝0， 　　所以直线l的斜率为0，其直线方程为y＝－1． 　　(2)因为抛物线以点F(0，1)为焦点，y＝－1为准线，设抛物线方程为x2＝2py，则＝1，p＝2． 　　故抛物线C的方程为x2＝4y． 　　解析：(1)依题意，要求直线l的方程，只需求其斜率即可，而直线l与曲线在x＝2处的切线平行，只要求出(2)即可；(2)设出抛物线方程，利用条件求出p即可．