题目内容
若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )
| A.k≤-3或-1≤k≤1或k≥3 | B.-3<k<-1或1<k<3 |
| C.-2<k<2 | D.不存在这样的实数 |
B
解析试题分析:由题意得,区间(k-1,k+1)内必须含有函数的导数的根2或-2,即k-1<2<k+1或k-1<-2<k+1,从而求出实数k的取值范围.解:由题意得,f′(x)=3x2-12 在区间(k-1,k+1)上至少有一个实数根,而f′(x)=3x2-12的根为±2,区间(k-1,k+1)的长度为2,故区间(k-1,k+1)内必须含有2或-2.∴k-1<2<k+1或k-1<-2<k+1,∴1<k<3 或-3<k<-1,故选 B
考点:函数的单调性与导数的关系
点评:本题考查函数的单调性与导数的关系,函数在区间上不是单调函数,则函数的导数在区间上有实数根

练习册系列答案
相关题目
若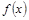 是偶函数,且当
是偶函数,且当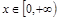 时,
时,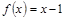 ,则
,则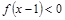 的解集是( )
的解集是( )
A.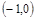 | B.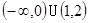 | C. | D.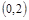 |
已知非零向量 ,
,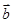 满足
满足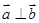 ,则函数
,则函数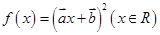 是 ( )
是 ( )
| A.偶函数 | B.奇函数 |
| C.既是奇函数又是偶函数 | D.非奇非偶函数 |
函数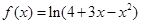 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B.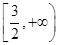 | C.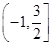 | D.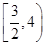 |
如图为函数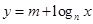 的图象,其中
的图象,其中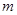 、
、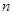 为常数,则下列结论正确( )
为常数,则下列结论正确( )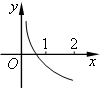
A. , ,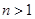 | B. , ,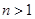 |
C. , , | D. , , |
下列函数中,既是 上的奇函数,又在
上的奇函数,又在 上单调递增的是( )
上单调递增的是( )
A.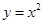 | B.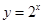 | C.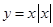 | D.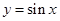 |
设函数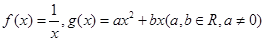 ,若
,若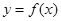 的图象与
的图象与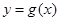 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点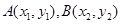 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.当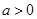 时, 时,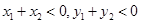 |
B.当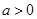 时, 时,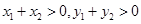 |
C.当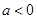 时, 时,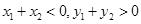 |
D.当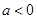 时, 时,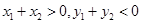 |
 在区间
在区间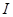 上有定义, 若
上有定义, 若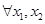
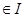 , 都有
, 都有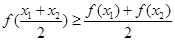 , 则称
, 则称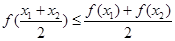 , 则称
, 则称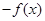 是区间
是区间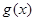 都是区间
都是区间 是区间
是区间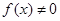 ,则
,则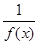 是区间
是区间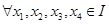 , 则有
, 则有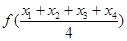
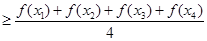
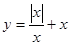 的图象是( )
的图象是( )