题目内容
已知椭圆x2+by2=3a与直线x+y-1=0相交于A、B两点
(1)当a=
时,求实数b的取值范围;
(2)当|AB|=2
时,AB的中点M与椭圆中心连线的斜率为
时,求椭圆的方程.
(1)当a=
| 1 |
| 4 |
(2)当|AB|=2
| 2 |
| 1 |
| 5 |
(1)解
得x2+b(1-x)2=3a
∴x2(1+b)-2bx+b-3a=0
由题意得:△=4b2-4(1+b)(b-3a)>0
解得b<3
又因为b>0且b≠1
∴0<b<3且b≠1
(2)设A(x1,y1) B(x2,y2) 由(1)x1+x2=
, x1x2=
∴|AB|=
,
=2
整理得:b2+3b-3a-3ab+1=0,
y1+y2=2-(x1+x2)=2-
=
AB中点M(
,
)
由题意得:KOM=
=
∴b=5
∴a=
所求椭圆方程为x2+5y2=
|
∴x2(1+b)-2bx+b-3a=0
由题意得:△=4b2-4(1+b)(b-3a)>0
解得b<3
又因为b>0且b≠1
∴0<b<3且b≠1
(2)设A(x1,y1) B(x2,y2) 由(1)x1+x2=
| 2b |
| 1+b |
| b-3a |
| 1+b |
∴|AB|=
| 1+1 |
|
| 2 |
整理得:b2+3b-3a-3ab+1=0,
y1+y2=2-(x1+x2)=2-
| 2b |
| 1+b |
| 2 |
| 1+b |
AB中点M(
| b |
| 1+b |
| 1 |
| 1+b |
由题意得:KOM=
| ||
|
| 1 |
| 5 |
∴a=
| 41 |
| 18 |
所求椭圆方程为x2+5y2=
| 41 |
| 6 |

练习册系列答案
相关题目
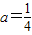 时,求实数b的取值范围;
时,求实数b的取值范围;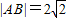 时,AB的中点M与椭圆中心连线的斜率为
时,AB的中点M与椭圆中心连线的斜率为 时,求椭圆的方程.
时,求椭圆的方程.