题目内容
若直线l的倾斜角α满足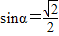 ,且直线l经过点P(4,2),则直线l的方程为 .
,且直线l经过点P(4,2),则直线l的方程为 .
【答案】分析:由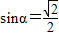 可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
解答:解:由 可得α=45°或135°,故tanα=1或-1,
可得α=45°或135°,故tanα=1或-1,
又直线过点P(4,2),故方程为y-2=x-4,或y-2=-(x-4)
化为一般式可得:x-y-2=0或x+y-6=0.
故答案为:x-y-2=0或x+y-6=0
点评:本题考查直线方程的求解,涉及分类的思想,属基础题.
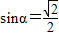 可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.解答:解:由
 可得α=45°或135°,故tanα=1或-1,
可得α=45°或135°,故tanα=1或-1,又直线过点P(4,2),故方程为y-2=x-4,或y-2=-(x-4)
化为一般式可得:x-y-2=0或x+y-6=0.
故答案为:x-y-2=0或x+y-6=0
点评:本题考查直线方程的求解,涉及分类的思想,属基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
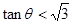 ,则θ的取值范围是( )
,则θ的取值范围是( )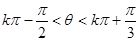 (k∈Z)
B、
(k∈Z)
B、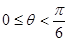 或
或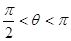
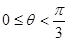 或
或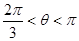
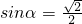 ,且直线l经过点P(4,2),则直线l的方程为________.
,且直线l经过点P(4,2),则直线l的方程为________.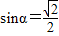 ,且直线l经过点P(4,2),则直线l的方程为 .
,且直线l经过点P(4,2),则直线l的方程为 .