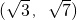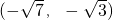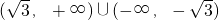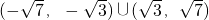题目内容
过点(0,4)的直线与双曲线 的右支交于A,B两点,则直线AB的斜率k的取值范围是( )
的右支交于A,B两点,则直线AB的斜率k的取值范围是( )A.

B.

C.

D.
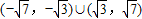
【答案】分析:如图:设过点(0,4)且与双曲线相切的直线为 l1,过点(0,4)且与渐近线y=-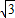 x平行的直线为l2.则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.把直线 l1 的方程代入双曲线的方程化简,由△=0,解得l1的斜率为
x平行的直线为l2.则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.把直线 l1 的方程代入双曲线的方程化简,由△=0,解得l1的斜率为 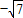 ,从而得到斜率k 的范围.
,从而得到斜率k 的范围.
解答:解:如图所示:过点(0,4)且与双曲线相切的直线为 l1,过点(0,4)且与渐近线y=-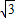 x平行的直线为l2.
x平行的直线为l2.
则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.
设直线 l1 的方程为y-4=k′(x-0),代入双曲线的方程化简得 (3-k2) x2-8kx-28-0.
由题意可得判别式△=0,解得 k′=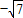 ,或 k′=
,或 k′=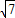 (舍去).
(舍去).
而l2的斜率等于-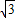 ,故直线AB的斜率k满足
,故直线AB的斜率k满足 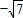 <k<
<k<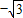 .
.
故选:B.
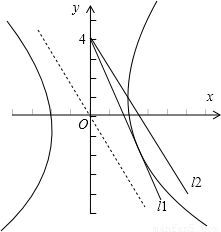
点评:本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,体现了数形结合的数学思想,判断直线AB的斜率k 应大于l1的斜率且小于l2的斜率,是解题的关键.
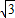 x平行的直线为l2.则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.把直线 l1 的方程代入双曲线的方程化简,由△=0,解得l1的斜率为
x平行的直线为l2.则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.把直线 l1 的方程代入双曲线的方程化简,由△=0,解得l1的斜率为 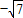 ,从而得到斜率k 的范围.
,从而得到斜率k 的范围.解答:解:如图所示:过点(0,4)且与双曲线相切的直线为 l1,过点(0,4)且与渐近线y=-
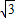 x平行的直线为l2.
x平行的直线为l2.则直线AB的斜率k 应大于l1的斜率且小于l2的斜率.
设直线 l1 的方程为y-4=k′(x-0),代入双曲线的方程化简得 (3-k2) x2-8kx-28-0.
由题意可得判别式△=0,解得 k′=
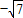 ,或 k′=
,或 k′=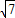 (舍去).
(舍去).而l2的斜率等于-
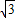 ,故直线AB的斜率k满足
,故直线AB的斜率k满足 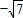 <k<
<k<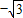 .
.故选:B.

点评:本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,体现了数形结合的数学思想,判断直线AB的斜率k 应大于l1的斜率且小于l2的斜率,是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目

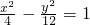 的右支交于A,B两点,则直线AB的斜率k的取值范围是
的右支交于A,B两点,则直线AB的斜率k的取值范围是