题目内容
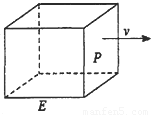
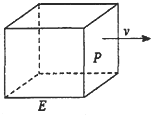 如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),物体E移动时单位时间内的淋雨量包括两部分:
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),物体E移动时单位时间内的淋雨量包括两部分:
①P或P的平行面(只有一个面淋雨)的淋雨量,设其值与|v-4|×S成正比,比例系数为 ;
;
②其它面的淋雨量之和,其值为 ,记y为物体E移动过程中的总淋雨量,当移动距离d=100,面积S=
,记y为物体E移动过程中的总淋雨量,当移动距离d=100,面积S= 时.
时.
(Ⅰ)写出y的表达式;
(Ⅱ)设0<v≤10,试确定移动速度v,使总淋雨量y最少.
解:(I)由题意知,E移动时单位时间内的淋雨量为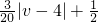 ,…(3分)
,…(3分)
故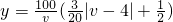 =
=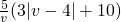 .…(6分)
.…(6分)
(II)由(I)知,当0<v≤4时,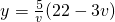 =
=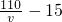
当4<v≤10时,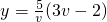 =
=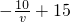
故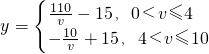 .…(10分)
.…(10分)
在(0,4]上,y是关于v的减函数;在(4,10]上,y是关于v的增函数; …(12分)
则当v=4时,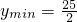 .
.
故移动速度v=4时,使总淋雨量y最少.…(14分)
分析:(Ⅰ)E移动时的总淋雨量应该等于单位时间内的淋雨量乘以所用的时间,可先求出单位时间内的淋雨量的式子,再乘以时间 即可;
即可;
(Ⅱ)根据绝对值的性质,将(Ⅰ)中的函数分解为分段函数的形式,再由v的不同取值范围讨论函数的单调性,在不同的情况下,单调区间不同,总淋雨量最小值对应的v值也不同.
点评:本题着重考查函数应用能力,所建立的函数式为含有绝对值的式子.解决问题的关键一是要能根据v的范围将式子化简为分段函数,二是要将常数v进行讨论得出函数的单调性,从而得出不同情形下的最小值点.
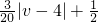 ,…(3分)
,…(3分)故
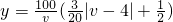 =
=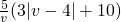 .…(6分)
.…(6分)(II)由(I)知,当0<v≤4时,
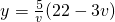 =
=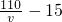
当4<v≤10时,
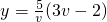 =
=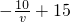
故
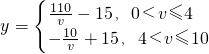 .…(10分)
.…(10分)在(0,4]上,y是关于v的减函数;在(4,10]上,y是关于v的增函数; …(12分)
则当v=4时,
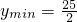 .
.故移动速度v=4时,使总淋雨量y最少.…(14分)
分析:(Ⅰ)E移动时的总淋雨量应该等于单位时间内的淋雨量乘以所用的时间,可先求出单位时间内的淋雨量的式子,再乘以时间
 即可;
即可;(Ⅱ)根据绝对值的性质,将(Ⅰ)中的函数分解为分段函数的形式,再由v的不同取值范围讨论函数的单调性,在不同的情况下,单调区间不同,总淋雨量最小值对应的v值也不同.
点评:本题着重考查函数应用能力,所建立的函数式为含有绝对值的式子.解决问题的关键一是要能根据v的范围将式子化简为分段函数,二是要将常数v进行讨论得出函数的单调性,从而得出不同情形下的最小值点.

练习册系列答案
相关题目
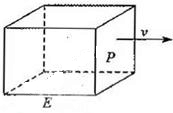 如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v-c|×S成正比,比例系数为
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v-c|×S成正比,比例系数为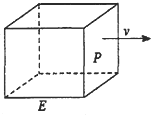 如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),物体E移动时单位时间内的淋雨量包括两部分:
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),物体E移动时单位时间内的淋雨量包括两部分: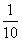 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为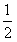 ,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=
,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=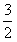 时。
时。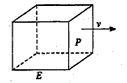
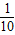 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=
,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S= 时.
时.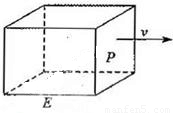
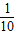 ;
; ,记y为物体E移动过程中的总淋雨量,当移动距离d=100,面积S=
,记y为物体E移动过程中的总淋雨量,当移动距离d=100,面积S= 时.
时.