题目内容
已知函数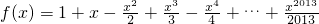 ,设F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则圆x2+y2=b-a的面积的最小值是________.
,设F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则圆x2+y2=b-a的面积的最小值是________.
π
分析:利用导数判断函数f(x)单调性,再利用函数零点的判定定理判断函数是否存在零点零点,利用平移变换找出F(x)与f(x)的零点之间的关系即可.
解答:∵f′(x)=1-x+x2+…+x2012,①x=0时,f′(0)=1>0;②当x=-1时,f′(-1)=2013>0;
③当x≠0,-1时,f′(x)= =
=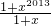 ,无论x>-1,还是x<-1,都有f′(x)>0.
,无论x>-1,还是x<-1,都有f′(x)>0.
综上可知:对?x∈R,都有f′(x)>0.∴函数f(x)单调递增,也就是说,函数f(x)至多有一个零点.
另一方面:f(0)=1>0,f(-1)═0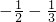 -…-
-…- <0,∴f(0)f(-1)<0,
<0,∴f(0)f(-1)<0,
由函数零点的判定定理可知:函数f(x)的零点x0∈(-1,0).
综上可知:函数f(x)有且只有一个零点x0∈(-1,0).
又F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,∴函数F(x)的零点 必在区间(-5,-4)内.
必在区间(-5,-4)内.
又(-5,-4)?[a,b],(a<b,a,b∈Z),∴b-a的最小值为1.
∴圆x2+y2=b-a的面积的最小值是π×12=π.
故答案为π.
点评:熟练掌握导数研究函数的单调性、函数零点的判定定理及平移变换是解题的关键.
分析:利用导数判断函数f(x)单调性,再利用函数零点的判定定理判断函数是否存在零点零点,利用平移变换找出F(x)与f(x)的零点之间的关系即可.
解答:∵f′(x)=1-x+x2+…+x2012,①x=0时,f′(0)=1>0;②当x=-1时,f′(-1)=2013>0;
③当x≠0,-1时,f′(x)=
 =
=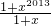 ,无论x>-1,还是x<-1,都有f′(x)>0.
,无论x>-1,还是x<-1,都有f′(x)>0.综上可知:对?x∈R,都有f′(x)>0.∴函数f(x)单调递增,也就是说,函数f(x)至多有一个零点.
另一方面:f(0)=1>0,f(-1)═0
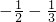 -…-
-…- <0,∴f(0)f(-1)<0,
<0,∴f(0)f(-1)<0,由函数零点的判定定理可知:函数f(x)的零点x0∈(-1,0).
综上可知:函数f(x)有且只有一个零点x0∈(-1,0).
又F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,∴函数F(x)的零点
 必在区间(-5,-4)内.
必在区间(-5,-4)内.又(-5,-4)?[a,b],(a<b,a,b∈Z),∴b-a的最小值为1.
∴圆x2+y2=b-a的面积的最小值是π×12=π.
故答案为π.
点评:熟练掌握导数研究函数的单调性、函数零点的判定定理及平移变换是解题的关键.

练习册系列答案
相关题目
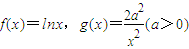 ,设F(x)=f(x)+g(x).
,设F(x)=f(x)+g(x).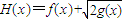 ,图象上任意一点P(x,y)为切点的切线的斜率k≤1恒成立,求实数a的最小值;
,图象上任意一点P(x,y)为切点的切线的斜率k≤1恒成立,求实数a的最小值;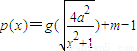 的图象与q(x)=f(1+x2)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.
的图象与q(x)=f(1+x2)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由. ,设f(x)的最大值、最小值分别为m,n,若m-n<1,则正整数a的取值个数是( )
,设f(x)的最大值、最小值分别为m,n,若m-n<1,则正整数a的取值个数是( )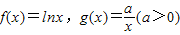 ,设F(x)=f(x)+g(x)
,设F(x)=f(x)+g(x)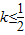 恒成立,求实数a的最小值;
恒成立,求实数a的最小值; ,设F(x)=x2•f(x),则F(x)是( )
,设F(x)=x2•f(x),则F(x)是( ) ,设F(x)=f(x)+g(x)
,设F(x)=f(x)+g(x)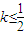 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;