题目内容
已知函数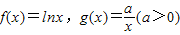 ,设F(x)=f(x)+g(x)
,设F(x)=f(x)+g(x)(1)求F(x)的单调区间;
(2)若以y=F(x)(x∈(0,3])图象上任意一点P(x,y)为切点的切线的斜率
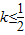 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;(3)若对所有的x∈[e,+∞)都有xf(x)≥ax-a成立,求实数a的取值范围.
【答案】分析:(1)先求出F(x),然后求出F'(x),分别求出F′(x)>0与F′(x)<0 求出F(x)的单调区间;
(2)利用导数的几何意义表示出切线的斜率k,根据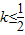 恒成立将a分离出来,
恒成立将a分离出来,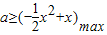 ,即可求出a的范围,从而得到a的最小值;
,即可求出a的范围,从而得到a的最小值;
(3)根据x≥e,所以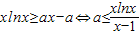 ,令
,令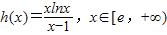 ,根据h'(x)的符号判定h(x)的单调性,求出最小值,即可求出a的范围.
,根据h'(x)的符号判定h(x)的单调性,求出最小值,即可求出a的范围.
解答:解:(1)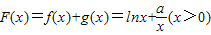 ,
,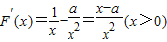 .(2分)
.(2分)
因为a>0由F′(x)>0⇒x∈(a,+∞),所以F(x)在上单调递增;由F′(x)<0⇒x∈(0,a),
所以F(x)在(0,a)上单调递减.(5分)
(2) 恒成立,(7分)
恒成立,(7分)
即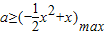 ,当x=1时取得最大值
,当x=1时取得最大值 .所以,
.所以,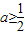 ,所以
,所以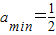 .(10分)
.(10分)
(3)因为x≥e,所以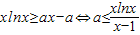 ,令
,令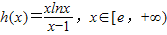 ,则
,则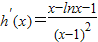 .(12分)
.(12分)
因为当x≥e时,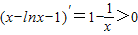 ,所以x-lnx-1≥e-lne-1=e-2>0,
,所以x-lnx-1≥e-lne-1=e-2>0,
所以h′(x)>0,所以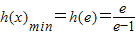 ,所以0<
,所以0<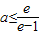 .(16分)
.(16分)
点评:本题主要考查了函数的单调性,以及在某点处的切线问题和函数恒成立问题等有关知识,同时考查了转化与划归的思想,属于综合题.
(2)利用导数的几何意义表示出切线的斜率k,根据
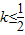 恒成立将a分离出来,
恒成立将a分离出来,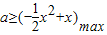 ,即可求出a的范围,从而得到a的最小值;
,即可求出a的范围,从而得到a的最小值;(3)根据x≥e,所以
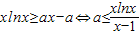 ,令
,令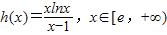 ,根据h'(x)的符号判定h(x)的单调性,求出最小值,即可求出a的范围.
,根据h'(x)的符号判定h(x)的单调性,求出最小值,即可求出a的范围.解答:解:(1)
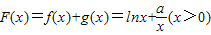 ,
,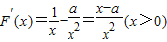 .(2分)
.(2分)因为a>0由F′(x)>0⇒x∈(a,+∞),所以F(x)在上单调递增;由F′(x)<0⇒x∈(0,a),
所以F(x)在(0,a)上单调递减.(5分)
(2)
 恒成立,(7分)
恒成立,(7分)即
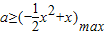 ,当x=1时取得最大值
,当x=1时取得最大值 .所以,
.所以,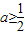 ,所以
,所以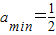 .(10分)
.(10分)(3)因为x≥e,所以
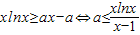 ,令
,令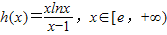 ,则
,则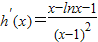 .(12分)
.(12分)因为当x≥e时,
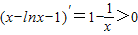 ,所以x-lnx-1≥e-lne-1=e-2>0,
,所以x-lnx-1≥e-lne-1=e-2>0,所以h′(x)>0,所以
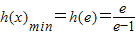 ,所以0<
,所以0<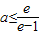 .(16分)
.(16分)点评:本题主要考查了函数的单调性,以及在某点处的切线问题和函数恒成立问题等有关知识,同时考查了转化与划归的思想,属于综合题.

练习册系列答案
相关题目
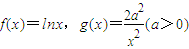 ,设F(x)=f(x)+g(x).
,设F(x)=f(x)+g(x).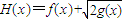 ,图象上任意一点P(x,y)为切点的切线的斜率k≤1恒成立,求实数a的最小值;
,图象上任意一点P(x,y)为切点的切线的斜率k≤1恒成立,求实数a的最小值;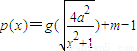 的图象与q(x)=f(1+x2)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.
的图象与q(x)=f(1+x2)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由. ,设f(x)的最大值、最小值分别为m,n,若m-n<1,则正整数a的取值个数是( )
,设f(x)的最大值、最小值分别为m,n,若m-n<1,则正整数a的取值个数是( ) ,设F(x)=x2•f(x),则F(x)是( )
,设F(x)=x2•f(x),则F(x)是( ) ,设F(x)=f(x)+g(x)
,设F(x)=f(x)+g(x)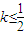 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;