题目内容
若向量 ,且
,且 ,则锐角
,则锐角 为( )
为( )
A. | B. | C. | D. |
A
解析试题分析:因为 ,所以
,所以 ,所以
,所以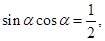 即
即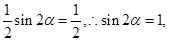
因为 为锐角,所以
为锐角,所以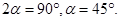
考点:本小题主要考查向量共线的坐标运算及二倍角公式的应用,考查学生的运算求解能力.
点评:向量共线与垂直是高考经常考查的两种关系,尤其是它们的坐标运算,要掌握公式,灵活应用.

练习册系列答案
相关题目
 ,则
,则 与
与 ( )
( )
| A.互相平行 | B.互相垂直 |
| C.夹角为30° | D.夹角为60° |
已知两个单位向量 的夹角为
的夹角为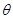 ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A. 方向上的投影为 方向上的投影为 | B. |
C. | D. |
若点 为
为 的重心,则下列各向量中与
的重心,则下列各向量中与 共线的是( )
共线的是( )
A. | B. |
C.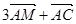 | D. |
已知向量 ,且
,且 ,则实数
,则实数 等于( )
等于( )
A. | B. | C. | D. |
单位向量 与
与 的夹角为
的夹角为 ,则
,则
A. | B. | C. | D. |
若│ │
│ ,│
,│ │
│ ,
,  与
与 的夹角为
的夹角为 ,则
,则 •
• 的值是( ).
的值是( ).
A.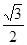 | B.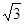 | C.2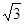 | D. |
 平面ABC的充分条件是 ( )
平面ABC的充分条件是 ( ) ; B.
; B. ;
; ; D.
; D.
 =(
=( b-c,cosC),
b-c,cosC), =(a,cosA),
=(a,cosA), B.-
B.- D.-
D.-