题目内容
(本题满分12分) 已知函数 的定义域为
的定义域为 .
.
(Ⅰ)求集合 ;
;
(Ⅱ)若函数 ,且
,且 ,求函数
,求函数 的最大最小值和对应的
的最大最小值和对应的 值;
值;
 的定义域为
的定义域为 .
.(Ⅰ)求集合
 ;
;(Ⅱ)若函数
 ,且
,且 ,求函数
,求函数 的最大最小值和对应的
的最大最小值和对应的 值;
值;(1)[1/2,4]
(2) 当
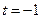 时,
时,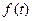 取得最大值,
取得最大值,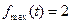 ,此时
,此时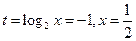
解:(Ⅰ)函数有意义,则有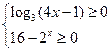 即:
即: 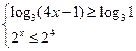
∵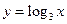 为
为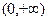 上的单调增函数,
上的单调增函数,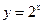 为
为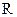 上的单调增函数
上的单调增函数

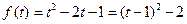 ,图象为开口向上二次函数,对称轴为
,图象为开口向上二次函数,对称轴为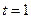 ,顶点坐标为
,顶点坐标为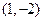
由图象可知,当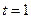 时,
时,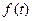 取得最小值,
取得最小值,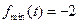 ,此时
,此时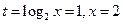 ;
;
当当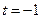 时,
时,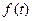 取得最大值,
取得最大值,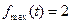 ,此时
,此时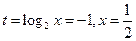 ………………12分
………………12分
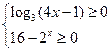 即:
即: 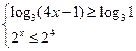
∵
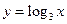 为
为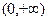 上的单调增函数,
上的单调增函数,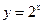 为
为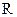 上的单调增函数
上的单调增函数
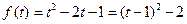 ,图象为开口向上二次函数,对称轴为
,图象为开口向上二次函数,对称轴为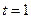 ,顶点坐标为
,顶点坐标为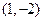
由图象可知,当
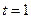 时,
时,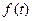 取得最小值,
取得最小值,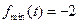 ,此时
,此时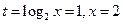 ;
;当当
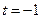 时,
时,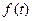 取得最大值,
取得最大值,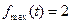 ,此时
,此时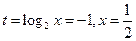 ………………12分
………………12分
练习册系列答案
相关题目
 ,则给出下列四个命题:①函数
,则给出下列四个命题:①函数 的定义域是R,值域为[0,1];②方程
的定义域是R,值域为[0,1];②方程 有无数个解;③函数
有无数个解;③函数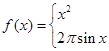
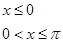 ,则集合
,则集合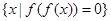 中元素的个数有 ( )
中元素的个数有 ( )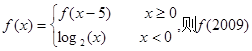 等于( )
等于( )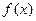 满足,
满足,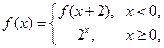 则
则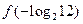 =
=
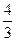


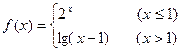 ,则
,则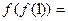 .
.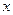 )=
)=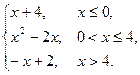 则f { f [ f (5)]}="_______" .
则f { f [ f (5)]}="_______" .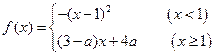 满足对任意
满足对任意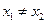 都有
都有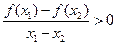 成立,则a的取值范围是 ▲ .
成立,则a的取值范围是 ▲ . 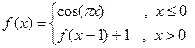 ,则
,则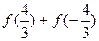 的值是____
的值是____