题目内容
投掷A,B,C三个纪念币,正面向上的概率如下表所示(0<a<1).
将这三个纪念币同时投掷一次,设ξ表示出现正面向上的个数.
(1)求ξ的分布列及数学期望;
(2)在概率P(ξ=i)(i=0,1,2,3)中,若P(ξ=1)的值最大,求a的取值范围.
分析:(1)由题意知本题是一个独立重复试验,看出变量的所有可能取值,根据独立重复试验的概率公式写出变量取不同值时的概率,写出分布列和期望.
(2)由题意知本题要使的P(ξ=1)的值最大,题目最容易考虑到的一种方法是把P(ξ=1)的值同其他几个变量的概率值进行比做差比较,使得差大于零,解不等式组,得到a的取值范围.
(2)由题意知本题要使的P(ξ=1)的值最大,题目最容易考虑到的一种方法是把P(ξ=1)的值同其他几个变量的概率值进行比做差比较,使得差大于零,解不等式组,得到a的取值范围.
解答:解:(1)由题意知ξ个正面向上,3-ξ个背面向上.
ξ的可能取值为0,1,2,3.
根据独立重复试验的概率公式得到变量的分布列,
P(ξ=0)=
(1-
)
(1-a)2=
(1-a)2,
P(ξ=1)=
•
(1-a)2+
(1-
)
a(1-a)=
(1-a2),P(ξ=2)=
•
a(1-a)+
(1-
)
a2=
(2a-a2),
P(ξ=3)=
•
a2=
.
∴ξ的分布列为

∴ξ的数学期望为Eξ=0×
(1-a)2+1×
(1-a2)+2×
(2a-a2)+3×
=
.
(2)P(ξ=1)-P(ξ=0)=
[(1-a2)-(1-a)2]=a(1-a),
P(ξ=1)-P(ξ=2)=
[(1-a2)-(2a-a2)]=
,
P(ξ=1)-P(ξ=3)=
[(1-a2)-a2]=
.
由
和0<a<1,
得0<a≤
,
即a的取值范围是(0,
].
ξ的可能取值为0,1,2,3.
根据独立重复试验的概率公式得到变量的分布列,
P(ξ=0)=
| C | 0 1 |
| 1 |
| 2 |
| C | 0 2 |
| 1 |
| 2 |
P(ξ=1)=
| C | 1 1 |
| 1 |
| 2 |
| C | 0 2 |
| C | 0 1 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
| C | 1 1 |
| 1 |
| 2 |
| C | 1 2 |
| C | 0 1 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 2 |
P(ξ=3)=
| C | 1 1 |
| 1 |
| 2 |
| C | 2 2 |
| a2 |
| 2 |
∴ξ的分布列为

∴ξ的数学期望为Eξ=0×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
| 4a+1 |
| 2 |
(2)P(ξ=1)-P(ξ=0)=
| 1 |
| 2 |
P(ξ=1)-P(ξ=2)=
| 1 |
| 2 |
| 1-2a |
| 2 |
P(ξ=1)-P(ξ=3)=
| 1 |
| 2 |
| 1-2a2 |
| 2 |
由
|
得0<a≤
| 1 |
| 2 |
即a的取值范围是(0,
| 1 |
| 2 |
点评:本题是一个综合题,解决离散型随机变量分布列问题时,主要依据概率的有关概念和运算,同时还要注意题目中离散型随机变量服从什么分布,若服从特殊的分布则运算要简单的多.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分10分)
投掷A,B,C三个纪念币,正面向上的概率如下表所示![]() .
.
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
将这三个纪念币同时投掷一次, 设![]() 表示出现正面向上的个数.
表示出现正面向上的个数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (i=0,1,2,3)中, 若
(i=0,1,2,3)中, 若![]() 的值最大, 求a的取值范围.
的值最大, 求a的取值范围.
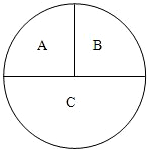 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
