题目内容
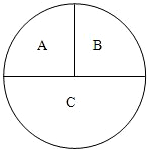 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.(Ⅰ)求该同学在一次投掷中投中A区域的概率;
(Ⅱ)设x表示该同学在3次投掷中投中A区域的次数,求x的分布列及数学期望;
(Ⅲ)若该同学投中A,B,C三个区域分别可得3分,2分,1分,求他投掷3次恰好得4分的概率.
分析:(1)题考查的知识点是几何概型的意义,关键是要找出满足条件A的区域面积和总面积之间的关系,再根据几何概型计算公式给出答案;(2)根据(1)中投中A区域的概率,不难列出x的分布列并进行数学期望;(3)考查的是古典概型,我们可以列举出三次投掷总的基本事件个数及恰得4分的事件个数,代入古典概型计算公式求解.
解答:解:(Ⅰ)设该同学在一次投掷中投中A区域的概率为P(A),
依题意,P(A)=
.
(Ⅱ)依题意知,X~B(3,
),P(X=k)=
(
)k(1-
)n-k(k=0,1,2,3)
从而X的分布列为:
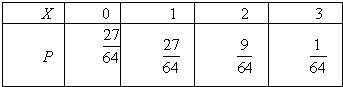
EX=np=
(Ⅲ)设Bi表示事件“第i次击中目标时,击中B区域”,Ci表示事件“第i次击中目标时,击中C区域”,i=1,2,3.
依题意知P=P(B1C2C3)+P(C1B2C3)+P(C1C2B3)=3×
×
×
=
.
依题意,P(A)=
| 1 |
| 4 |
(Ⅱ)依题意知,X~B(3,
| 1 |
| 4 |
| C | k n |
| 1 |
| 4 |
| 1 |
| 4 |
从而X的分布列为:

EX=np=
| 3 |
| 4 |
(Ⅲ)设Bi表示事件“第i次击中目标时,击中B区域”,Ci表示事件“第i次击中目标时,击中C区域”,i=1,2,3.
依题意知P=P(B1C2C3)+P(C1B2C3)+P(C1C2B3)=3×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
点评:求古典概型的概率的基本步骤为:(1)算出所有基本事件的个数n.(2)求出事件A包含的所有基本事件数m.(3)代入公式,求出P(A).几何概型中的三种基本度量为长度、面积和体积,在解题时要准确把握,要把问题向它们作合理地转化,要注意古典概型与几何概型的区别(基本事件的有限性和无限性),正确选用几何概型解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
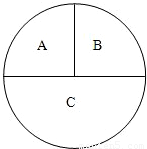 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.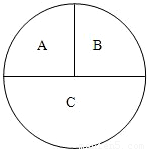 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的. 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.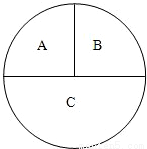 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.