题目内容
已知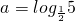
，b=log23，c=1，d=3-0.5，那么
- A.d＜a＜c＜b
- B.d＜c＜a＜b
- C.a＜b＜c＜d
- D.a＜d＜c＜b
D
分析：由函数y=
，y=log2x和y=3x的单调性可得a＜0，b＞1，0＜d＜1，可得答案．
解答：因为对数函数y=单调递减，故＜
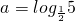=0；
同理因为对数函数y=log2x单调递增，故b=log23＞log22=1；
由指数函数y=3x单调递增，故0＜d=3-0.5＜30=1，
综上可得a＜d＜c＜b，
故选D
点评：本题考查数值大小的比较，涉及指数函数和对数函数的单调性，属基础题．
分析：由函数y=
，y=log2x和y=3x的单调性可得a＜0，b＞1，0＜d＜1，可得答案．解答：因为对数函数y=
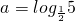单调递减，故＜=0；同理因为对数函数y=log2x单调递增，故b=log23＞log22=1；
由指数函数y=3x单调递增，故0＜d=3-0.5＜30=1，
综上可得a＜d＜c＜b，
故选D
点评：本题考查数值大小的比较，涉及指数函数和对数函数的单调性，属基础题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
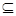{0,1,2,log23} D.不存在满足条件的集合
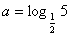，b=log23，c=1，d=3-0.2，则a，b，c，d的大小关系是