题目内容
【题目】在△ABC中,A,B的坐标分别是 ![]() ,点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|. (Ⅰ)求△ABC的顶点C的轨迹E的方程;
,点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|. (Ⅰ)求△ABC的顶点C的轨迹E的方程;
(Ⅱ)直线l:y=kx+m与轨迹E相交于P,Q两点,若在轨迹E上存在点R,使四边形OPRQ为平行四边形(其中O为坐标原点),求m的取值范围.
【答案】解:(Ⅰ)设C(x,y),∵点G是△ABC的重心, ∴G ![]() ,
,
∵y轴上一点M满足GM∥AB,∴ ![]() .
.
∵|MC|=|MB|,
∴ 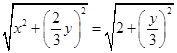 ,
,
化为 ![]() 即为△ABC的顶点C的轨迹E的方程;
即为△ABC的顶点C的轨迹E的方程;
(Ⅱ)设P(x1 , y1),Q(x2 , y2),联立 ![]() ,化为(3+k2)x2+2kmx+m2﹣6=0,
,化为(3+k2)x2+2kmx+m2﹣6=0,
由△>0,化为 2k2﹣m2+6>0,
∴ ![]() ,
, ![]() .
.
∵四边形OPRQ为平行四边形,
∴ ![]() ,
,
∴R(x1+x2 , y1+y2),y1+y2=k(x1+x2)+2m= ![]() ,
,
∴R ![]() .
.
∵点R在椭圆上,
∴ ![]() =6,化为2m2=k2+3.
=6,化为2m2=k2+3.
代入△>0,可得m2>0,
又2m2≥3,解得 ![]() 或m
或m ![]() .
.
∴m的取值范围是 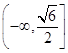 ∪
∪ 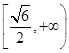
【解析】(Ⅰ)设C(x,y),由点G是△ABC的重心,可得G ![]() ,由y轴上一点M满足GM∥AB,可得
,由y轴上一点M满足GM∥AB,可得 ![]() .由|MC|=|MB|,利用两点之间的距离公式可得
.由|MC|=|MB|,利用两点之间的距离公式可得 ![]() ,即可得出;(Ⅱ)设P(x1 , y1),Q(x2 , y2),与椭圆方程联立化为(3+k2)x2+2kmx+m2﹣6=0,由△>0,可得 2k2﹣m2+6>0,由四边形OPRQ为平行四边形,可得
,即可得出;(Ⅱ)设P(x1 , y1),Q(x2 , y2),与椭圆方程联立化为(3+k2)x2+2kmx+m2﹣6=0,由△>0,可得 2k2﹣m2+6>0,由四边形OPRQ为平行四边形,可得 ![]() ,可得R(x1+x2 , y1+y2),利用根与系数的关系可得R
,可得R(x1+x2 , y1+y2),利用根与系数的关系可得R ![]() .由点R在椭圆上,代入椭圆方程化为2m2=k2+3.结合△>0,即可解出m的取值范围.
.由点R在椭圆上,代入椭圆方程化为2m2=k2+3.结合△>0,即可解出m的取值范围.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目