题目内容
已知双曲线的渐近线的方程为2x±3y=0.
(1)若双曲线经过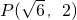 ,求双曲线方程;
,求双曲线方程;
(2)若双曲线的焦距是 ,求双曲线方程.
,求双曲线方程.
解:(1)∵双曲线的渐近线的方程为2x±3y=0.
∴设双曲线方程为:4x2-9y2=λ(λ≠0)
∵双曲线经过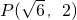 ,
,
∴4×( )2-9×22=λ,得λ=-12,
)2-9×22=λ,得λ=-12,
可得双曲线方程为:4x2-9y2=-12,化为标准形式得: .
.
(2)①当双曲线焦点在x轴上时,设方程为
∵渐近线的方程为2x±3y=0且焦距是 ,
,
∴ ,解之得a=3,b=2.因此双曲线方程为
,解之得a=3,b=2.因此双曲线方程为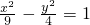
②当双曲线焦点在y轴上时,设方程为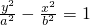
用类似于①的方法,可解得a=2,b=3.因此双曲线方程为
综上所述,可得双曲线方程为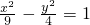 或
或 .
.
分析:(1)根据据题意,可设双曲线方程为4x2-9y2=λ(λ≠0),将已知点P的坐标代入可得λ的值,即可得到双曲线的方程,最后再化成标准方程;
(2)分双曲线焦点在x轴和y轴进行讨论,根据题意建立关于a、b的方程组,联解可得a、b的值,从而得到双曲线的方程.
点评:本题给出双曲线的渐近线方程,求双曲线的标准方程,着重考查了双曲线的基本概念和简单几何性质的知识,属于基础题.
∴设双曲线方程为:4x2-9y2=λ(λ≠0)
∵双曲线经过
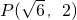 ,
,∴4×(
 )2-9×22=λ,得λ=-12,
)2-9×22=λ,得λ=-12,可得双曲线方程为:4x2-9y2=-12,化为标准形式得:
 .
.(2)①当双曲线焦点在x轴上时,设方程为

∵渐近线的方程为2x±3y=0且焦距是
 ,
,∴
 ,解之得a=3,b=2.因此双曲线方程为
,解之得a=3,b=2.因此双曲线方程为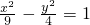
②当双曲线焦点在y轴上时,设方程为
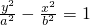
用类似于①的方法,可解得a=2,b=3.因此双曲线方程为

综上所述,可得双曲线方程为
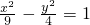 或
或 .
.分析:(1)根据据题意,可设双曲线方程为4x2-9y2=λ(λ≠0),将已知点P的坐标代入可得λ的值,即可得到双曲线的方程,最后再化成标准方程;
(2)分双曲线焦点在x轴和y轴进行讨论,根据题意建立关于a、b的方程组,联解可得a、b的值,从而得到双曲线的方程.
点评:本题给出双曲线的渐近线方程,求双曲线的标准方程,着重考查了双曲线的基本概念和简单几何性质的知识,属于基础题.

练习册系列答案
相关题目