题目内容
已知函数f(x)=mx-![]() ,g(x)=2lnx.
,g(x)=2lnx.
(Ⅰ)当m=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)当m=1时,证明方程f(x)=g(x)有且仅有一个实数根;
(Ⅲ)若xÎ (1,e]时,不等式f(x)-g(x)<2恒成立,求实数m的取值范围.
答案:
解析:
解析:
|
解:(1)m=2时,f(x)=2x- 切点坐标为(1,0),∴切线方程为y=4x-4 2分 (2)m=1时,令h(x)=f(x)-g(x)=x- ∴h(x)在(0,+∞)上是增函数 4分 又h(e)·h( ∴方程 (或说明h(1)=0也可以) (3)由题意知,mx- 则当xÎ
(1,e]时,m< 令G(x)= 则G(x)在xÎ
(1,e]时递减,∴G(x)在xÎ
(1,e]时的最小值为G(e)= 则m的取值范围是(-∞, |

练习册系列答案
相关题目
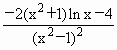 <0 9分
<0 9分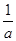 +
+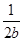 +
+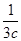 =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9. (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2. ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.