题目内容
已知函数f(x)=(m,n∈R)在x=1处取到极值2.
(1)求f(x)的解析式;
(2)设函数g(x)=ax-lnx.若对任意的x1∈[,2],总存在唯一的x2∈[,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
【答案】
解: (1)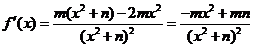 …………………………2分
…………………………2分
由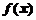 在
在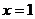 处取到极值2,故
处取到极值2,故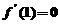 ,
,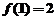 即
即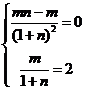 ,
,
解得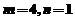 ,经检验,此时
,经检验,此时 在
在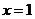 处取得极值.故
处取得极值.故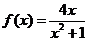 ……5分
……5分
(2)由(1)知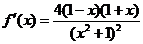 ,故
,故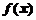 在
在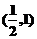 上单调递增,在
上单调递增,在
 上单调递减,由
上单调递减,由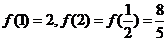 ,故
,故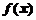 的值域为
的值域为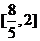 …………………………7分
…………………………7分
依题意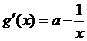 ,记
,记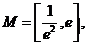
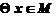
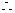
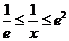
(ⅰ)当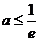 时,
时,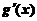
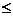
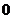 ,
,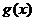 在
在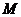 上单调递减,
上单调递减,
依题意由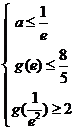 ,得
,得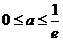 ,……………………………………………………8分
,……………………………………………………8分
(ⅱ)当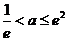 时,
时,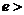
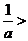
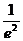 当
当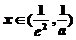 时,
时,
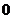 ,当
,当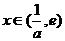 时,
时,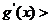
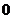
依题意得: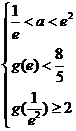 或
或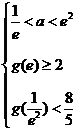 ,解得
,解得 ,…………………………10分
,…………………………10分
(ⅲ)当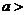
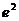 时,
时,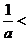
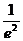 ,此时
,此时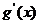
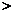
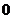 ,
,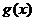 在
在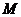 上单调递增依题意得
上单调递增依题意得
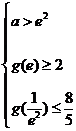 即
即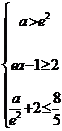 此不等式组无解 ……………………………………11分.
此不等式组无解 ……………………………………11分.
综上,所求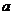 取值范围为
取值范围为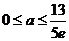 ………………………………………………14分
………………………………………………14分

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有