题目内容
将n件不同的产品排成一排,若其中A,B两件产品排在一起的不同排法有48种,则n=________.
5
解析试题分析:两件产品排在一起,常用的方法是捆绑法,先将A,B绑在一起看作一个元素,则问题转化为n-1个元素的排列数,令其值为48,解此方程求出n的值. 解:本问题的计数可以分为两步完成,先将A,B两元素捆绑,有A22=2种排法,第二步将AB两元素看作是一个元素,与其余的元素组成n-1个元素,其排法为(n-1)!
由乘法原理知总的排法有2×(n-1)!,又总的排法有48种,故有(n-1)!=24,,∵4×3×2=24,∴n-1=4,即n=5,故答案为5
考点:排列组合的运用
点评:本题考查排列组合及简单计数问题,解题的关键是理解本题中计数问题,找到合适的计数方法建立方程,熟练掌握排列公式以及分步乘法计数原理是解本题的知识保证,本题是计数原理的应用题,其考查方法是利用计数原理建立方程求出n的值,是对排列与计数原理考查的一种变式题,注意总结此类题的解法规律

练习册系列答案
相关题目
 的展开式中恰好第5项的二项式系数最大,则它的常数项是 .
的展开式中恰好第5项的二项式系数最大,则它的常数项是 .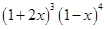 展开式中
展开式中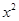 的系数为________。(用数字作答)
的系数为________。(用数字作答) 展开式中二项式系数之和是1024,常数项为180,则实数
展开式中二项式系数之和是1024,常数项为180,则实数 的值是 .
的值是 .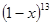 展开式中含
展开式中含 的奇次项的系数和为 。
的奇次项的系数和为 。 的展开式中的常数项为___ __.
的展开式中的常数项为___ __.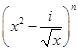 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-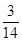 ,其中
,其中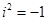 ,则展开式中常数项是 。
,则展开式中常数项是 。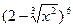 的展开式中
的展开式中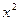 项的系数为__________.
项的系数为__________.