题目内容
如果f(x)在某个区间I内满足:对任意的x1,x2∈I,都有
[f(x1)+f(x2)]≥f(
),则称f(x)在I上为下凸函数;已知函数f(x)=
-alnx.
(Ⅰ)证明:当a>0时,f(x)在(0,+∞)上为下凸函数;
(Ⅱ)若f'(x)为f(x)的导函数,且x∈[
,2]时,|f'(x)|<1,求实数a的取值范围.
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| x |
(Ⅰ)证明:当a>0时,f(x)在(0,+∞)上为下凸函数;
(Ⅱ)若f'(x)为f(x)的导函数,且x∈[
| 1 |
| 2 |
分析:(Ⅰ)由题设中的定义知,可先得出
[f(x1)+f(x2)]与f(
)的展开式,整理成最简形式,根据题设条件判断出
[f(x1)+f(x2)]≥f(
)即可证明出结论;
(II)由题意f'(x)为f(x)的导函数,且x∈[
,2]时,|f'(x)|<1可得出-(x+
)<a<x-
,由于在x∈[
,2]时,此不等式恒成立,故可构造出两个函数g(x)=-(x+
),h(x)=x-
,将问题转化为gmax(x)<a<hmin(x),根据两函数的单调性求出gmax(x)与hmin(x),即可得到a的取值范围.
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
(II)由题意f'(x)为f(x)的导函数,且x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
解答:解:(Ⅰ)任取x1,x2∈(0,+∞),则
[f(x1)+f(x2)]=
[
-alnx1+
-alnx2]=
-aln
,…(2分)
f(
)=
-aln
,…(3分)
∵x12+x22≥2x1x2,∴(x1+x2)2≥4x1x2,
又x1>0,x2>0,
≥
,…(5分)
又
≥
,a>0,
∴-aln
≥aln
,
即
[f(x1)+f(x2)]≥f(
).
∴f(x)为(0,+∞)上的下凸函数…(7分)
答:f(x)为(0,+∞)上的下凸函数
(Ⅱ)先对所给的函数求导得到f′(x)=-
-
,…(9分)
∵|f′(x)|<1,即|
+
|<1,
∴-(x+
)<a<x-
,…(11分)
∵x∈[
,2]时,|f′(x)|<1恒成立,
设g(x)=-(x+
),h(x)=x-
则有gmax(x)<a<hmin(x),
又g(x)=-(x+
)在[
,1]上为增函数,在[1,2]上为减函数
∴gmax(x)=g(1)=-2…(12分),
而h(x)=x-
在[
,2]上为增函数,
∴hmin(x)=h(
)=-
…(13分)
∴a∈(-2,-
)…(14分)
答:实数a的取值范围是(-2,-
)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| 2x1x2 |
| x1x2 |
f(
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2 |
∵x12+x22≥2x1x2,∴(x1+x2)2≥4x1x2,
又x1>0,x2>0,
| x1+x2 |
| 2x1x2 |
| 2 |
| x1+x2 |
又
| x1+x2 |
| 2 |
| x1x2 |
∴-aln
| x1x2 |
| x1+x2 |
| 2 |
即
| 1 |
| 2 |
| x1+x2 |
| 2 |
∴f(x)为(0,+∞)上的下凸函数…(7分)
答:f(x)为(0,+∞)上的下凸函数
(Ⅱ)先对所给的函数求导得到f′(x)=-
| 1 |
| x2 |
| a |
| x |
∵|f′(x)|<1,即|
| 1 |
| x2 |
| a |
| x |
∴-(x+
| 1 |
| x |
| 1 |
| x |
∵x∈[
| 1 |
| 2 |
设g(x)=-(x+
| 1 |
| x |
| 1 |
| x |
则有gmax(x)<a<hmin(x),
又g(x)=-(x+
| 1 |
| x |
| 1 |
| 2 |
∴gmax(x)=g(1)=-2…(12分),
而h(x)=x-
| 1 |
| x |
| 1 |
| 2 |
∴hmin(x)=h(
| 1 |
| 2 |
| 3 |
| 2 |
∴a∈(-2,-
| 3 |
| 2 |
答:实数a的取值范围是(-2,-
| 3 |
| 2 |
点评:本题是一个新定义的题,考查了利用新定义证明,利用不等式恒成立求参数的取值范围,理解新定义,将恒成立的问题进行正确转化是解题的关键,利用导数求最值是导数的重要运用,本题用到了转化的思想,函数的思想,是综合性较强的题,可能因为找不到问题的转化方向而无法下手.

练习册系列答案
相关题目
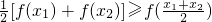 ,则称f(x)在I上为下凸函数;已知函数
,则称f(x)在I上为下凸函数;已知函数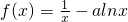 .
.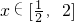 时,|f'(x)|<1,求实数a的取值范围.
时,|f'(x)|<1,求实数a的取值范围. ,则称f(x)在I上为下凸函数;已知函数
,则称f(x)在I上为下凸函数;已知函数 .
. 时,|f'(x)|<1,求实数a的取值范围.
时,|f'(x)|<1,求实数a的取值范围.