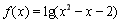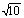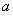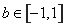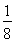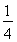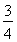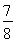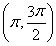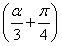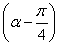题目内容
已知a,b∈R,函数f(x)=a+ln(x+1)的图象与g(x)= x3-
x3-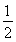 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.
(1)证明:不等式f(x)≤g(x)对一切x∈(-1,+∞)恒成立;
(2)设-1<x1<x2,当x∈(x1,x2)时,证明: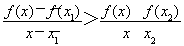 .
.
(1)见解析(2)见解析
【解析】(1)由题意得f′(x)=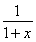 ,g′(x)=x2-x+b,x>-1,
,g′(x)=x2-x+b,x>-1,
则 解得
解得
∴f(x)=ln(x+1)(x>-1),g(x)=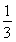 x3-
x3- x2+x.
x2+x.
令h(x)=f(x)-g(x)
=ln(x+1)- x3+
x3+ x2-x(x>-1),
x2-x(x>-1),
∴h′(x)=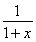 -x2+x-1=-
-x2+x-1=-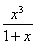 ,
,
∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴h(x)≤h(0)=0,∴f(x)≤g(x).
(2)当x∈(x1,x2)时,由题意得-1<x1<x<x2,
①设u(x)=(x+1)[f(x)-f(x1)]-(x-x1),
则u′(x)=ln(x+1)-ln(x1+1)>0,
∴u(x)>u(x1)=0,即(x+1)[f(x)-f(x1)]-(x-x1)>0,
∴ ;
;
②设v(x)=(x+1)[f(x)-f(x2)]-(x-x2),
则v′(x)=ln(x+1)-ln(x2+1)<0,
∴v(x)>v(x2)=0,即(x+1)[f(x)-f(x2)]-(x-x2)>0,
∴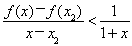 ,
,
由①②得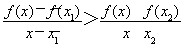 .
.

练习册系列答案
相关题目
一次射击训练,某小组的成绩只有7环、8环、9环三种情况,且该小组的平均成绩为8.15环,设该小组成绩为7环的有x人,成绩为8环、9环的人数情况见下表:
环数(环) | 8 | 9 |
人数(人) | 7 | 8 |
那么x=________.