Question

对于函数y=f(x)，若x₁+x₂=1, 则f(x₁)+f(x₂)=1,记数列f(),f(),

……,f()……,(n≥2，n∈)的前n项的和为S_{n ；}

   (1)求S_n;

   (2)若a=,a=   (n≥2，n∈),

Answer 1

（1）S_n=(n≥2,n∈N^*).

         (2)λ的最小值为

解析:

（1）由已知 x₁+x₂=1,f(x₁)+f(x₂)=1,

       S_n=f( 

     又 S_n=f(,

   2S_n=［f()+［f()+…+［f() =n-1

     ∴S_n=(n≥2,n∈N^*).

  (2)当n≥2时,a_n=

     T_n=(       由T_n≤λ(S_n+1+1)得

     λ≥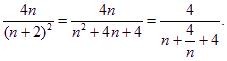

    ∵n+≥4,当且仅当n=2时等号成立,   ∴

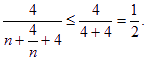
    故   λ的最小值为