题目内容
【题目】已知平面内两点A(8,-6),B(2,2).
（1）求过点P(2,-3)且与直线AB平行的直线l的方程;
（2）一束光线从B点射向(1)中直线l，若反射光线过点A,求反射光线所在的直线方程.
【答案】
（1）解：由点斜式 
∴直线l的方程4x+3y+1=0
（2）解：设B（2，2）关于直线l的对称点B'（m，n）∴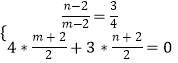 
解得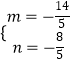 
∴ 
；
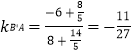由点斜式可得 
整理得11x+27y+74=0
【解析】(1)由题意借助两个点的坐标求出A、B两点所在直线的方程，再利用点斜式求出过点P(2,-3)且与直线AB平行的直线l的方程。(2)根据入射光线和反射光线的性质，利用点关于直线对称即可求出点B（2，2）关于直线l的对称点B'的坐标，所以就可以求出 kB'A的值再利用点斜式求出直线的方程。
【考点精析】认真审题，首先需要了解两条直线平行与倾斜角、斜率的关系(两条直线都有斜率而且不重合，如果它们平行，那么它们的斜率相等；反之，如果它们的斜率相等，那么它们平行)，还要掌握点斜式方程(直线的点斜式方程：直线
经过点
，且斜率为
则：
)的相关知识才是答题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
