题目内容
若实数x，y满足（x+5）2+（y-12）2=142，则x2+y2的最小值为（ ）A．2
B．1
C．
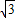
D．
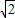
【答案】分析：确定方程（x+5）2+（y-12）2=142的几何意义，x2+y2的几何意义，即可求得结论．
解答：解：方程（x+5）2+（y-12）2=142表示以（-5，12）为圆心，14为半径的圆，x2+y2表示圆上的点到原点距离的平方
∵圆心到原点的距离为13
∴
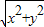的最小值为14-13=1
∴x2+y2的最小值为1
故选B
点评：本题考查距离公式的运用，考查圆的方程的几何意义，属于基础题．
解答：解：方程（x+5）2+（y-12）2=142表示以（-5，12）为圆心，14为半径的圆，x2+y2表示圆上的点到原点距离的平方
∵圆心到原点的距离为13
∴
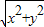的最小值为14-13=1∴x2+y2的最小值为1
故选B
点评：本题考查距离公式的运用，考查圆的方程的几何意义，属于基础题．
练习册系列答案
相关题目
若实数x、y满足条件
，则
的最大值为（ ）
|
| y |
| x |
A、9-4
| ||
| B、5 | ||
| C、3 | ||
| D、1 |