题目内容
甲乙二人进行射击练习,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,
,(1)若甲乙各射击3次,求甲恰好比乙多击中目标2次的概率;
(2)甲乙各射击n次,为使目标被击中的概率大于0.99,求n的最小值.
【答案】分析:(1)先求得甲击中目标2次,而乙一次也没有击中目标的概率为 
 •(1-
•(1- )•
)•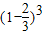 ;甲击中目标3次,而乙只击中一次的概率为
;甲击中目标3次,而乙只击中一次的概率为 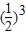 •
•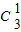

 ,
,
相加即得所求.
(2)射击n次,求得目标没有被击中的概率为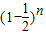 •
•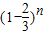 ,可得目标被击中的概率为 1-
,可得目标被击中的概率为 1-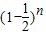 •
• >0.99,由此求得自然数n的最小值.
>0.99,由此求得自然数n的最小值.
解答:解:(1)甲恰好比乙多击中目标2次,即甲击中目标2次,而乙一次也没有击中目标;或者甲击中目标3次,而乙只击中一次.
甲击中目标2次,而乙一次也没有击中目标的概率为
 •(1-
•(1- )•
)• =
= ;
;
甲击中目标3次,而乙只击中一次的概率为 •
•

 =
= ,
,
∴甲恰好比乙多击中目标2次的概率为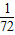 +
+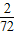 =
= .
.
(2)射击n次,目标没有被击中的概率为 •
•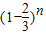 ,则目标被击中的概率为 1-
,则目标被击中的概率为 1- •
• >0.99,
>0.99,
经过检验,自然数n的最小值为3.
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件的概率等于用1减去它的对立事件概率,属于中档题.

 •(1-
•(1- )•
)•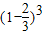 ;甲击中目标3次,而乙只击中一次的概率为
;甲击中目标3次,而乙只击中一次的概率为 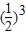 •
•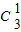

 ,
,相加即得所求.
(2)射击n次,求得目标没有被击中的概率为
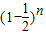 •
•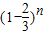 ,可得目标被击中的概率为 1-
,可得目标被击中的概率为 1-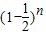 •
• >0.99,由此求得自然数n的最小值.
>0.99,由此求得自然数n的最小值.解答:解:(1)甲恰好比乙多击中目标2次,即甲击中目标2次,而乙一次也没有击中目标;或者甲击中目标3次,而乙只击中一次.
甲击中目标2次,而乙一次也没有击中目标的概率为

 •(1-
•(1- )•
)• =
= ;
;甲击中目标3次,而乙只击中一次的概率为
 •
•

 =
= ,
,∴甲恰好比乙多击中目标2次的概率为
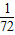 +
+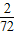 =
= .
.(2)射击n次,目标没有被击中的概率为
 •
•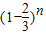 ,则目标被击中的概率为 1-
,则目标被击中的概率为 1- •
• >0.99,
>0.99,经过检验,自然数n的最小值为3.
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件的概率等于用1减去它的对立事件概率,属于中档题.

练习册系列答案
相关题目