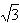题目内容
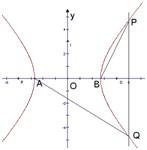 A、B是双曲线C的两个顶点,直线l与实轴垂直,与双曲线C交于P、Q两点,若
A、B是双曲线C的两个顶点,直线l与实轴垂直,与双曲线C交于P、Q两点,若| PB |
| AQ |
分析:设双曲线方程为
-
=1(a>0,b>0),由
•
=0得(a-x,-y)•(x+a,-y)=0从而x2-y2=a2,又因点P在双曲线上,满足
-
=1,由此可知双曲线C的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| PB |
| AQ |
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:设双曲线方程为
-
=1(a>0,b>0),双曲线上点P(x,y),
则A(-a,0),B(a,0),Q(x,-y).
由
•
=0得(a-x,-y)•(x+a,-y)=0从而x2-y2=a2,
又因点P在双曲线上,满足
-
=1,
另从题中知点P为任意可由两式比较得a2=b2,则双曲线C的离心率e=
.
答案:
.
| x2 |
| a2 |
| y2 |
| b2 |
则A(-a,0),B(a,0),Q(x,-y).
由
| PB |
| AQ |
又因点P在双曲线上,满足
| x2 |
| a2 |
| y2 |
| b2 |
另从题中知点P为任意可由两式比较得a2=b2,则双曲线C的离心率e=
| 2 |
答案:
| 2 |
点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
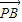 •
•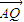 =0,则双曲线C的离心率e= .
=0,则双曲线C的离心率e= .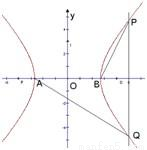
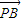 •
•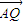 =0,则双曲线C的离心率e= .
=0,则双曲线C的离心率e= .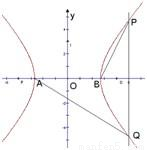
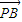 •
•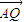 =0,则双曲线C的离心率e= .
=0,则双曲线C的离心率e= .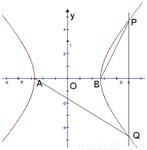
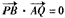 ,则双曲线C的离心率e为
,则双曲线C的离心率e为