题目内容
非空集合G关于运算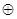 满足:(1)对任意的
满足:(1)对任意的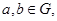 都有
都有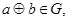 (2)存在
(2)存在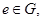 都有
都有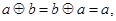 则称G关于运算
则称G关于运算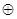 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①G={非负整数},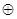 为整数的加法。
为整数的加法。
②G={偶数},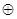 为整数的乘法。
为整数的乘法。
③G={平面向量},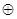 为平面向量的加法。
为平面向量的加法。
④G={虚数},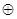 为复数的乘法。
为复数的乘法。
其中G关于运算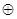 为“融洽集”的是________。(写出所有“融洽集”的序号)
为“融洽集”的是________。(写出所有“融洽集”的序号)
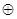 满足:(1)对任意的
满足:(1)对任意的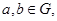 都有
都有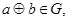 (2)存在
(2)存在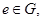 都有
都有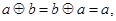 则称G关于运算
则称G关于运算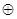 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:①G={非负整数},
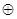 为整数的加法。
为整数的加法。②G={偶数},
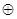 为整数的乘法。
为整数的乘法。③G={平面向量},
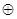 为平面向量的加法。
为平面向量的加法。④G={虚数},
 为复数的乘法。
为复数的乘法。其中G关于运算
 为“融洽集”的是________。(写出所有“融洽集”的序号)
为“融洽集”的是________。(写出所有“融洽集”的序号)①③
解:①G={非负整数},⊕为整数的加法,满足任意a,b∈G,都有a⊕b∈G,
且令e=0,有a⊕0=0⊕a=a,∴①符合要求;
②G={偶数},⊕为整数的乘法,若存在a⊕e=a×e=a,则e=1,矛盾,∴②不符合要求;
③G={平面向量},⊕为平面向量的加法,两个向量相加结果仍为向量;取e=0
,满足要求,∴③符合要求;
④G={二次三项式},⊕为多项式的加法,两个二次三项式相加得到的可能不是二次三项式,
∴④不符合要求;
⑤G={虚数},⊕为复数的乘法,两个虚数相乘得到的可能是实数,∴⑤不符合要求,
这样G关于运算⊕为“融洽集”的有①③.
故答案为:①③.
且令e=0,有a⊕0=0⊕a=a,∴①符合要求;
②G={偶数},⊕为整数的乘法,若存在a⊕e=a×e=a,则e=1,矛盾,∴②不符合要求;
③G={平面向量},⊕为平面向量的加法,两个向量相加结果仍为向量;取e=0
④G={二次三项式},⊕为多项式的加法,两个二次三项式相加得到的可能不是二次三项式,
∴④不符合要求;
⑤G={虚数},⊕为复数的乘法,两个虚数相乘得到的可能是实数,∴⑤不符合要求,
这样G关于运算⊕为“融洽集”的有①③.
故答案为:①③.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 ,求
,求 成立时
成立时 的取值范围。
的取值范围。 ,
, ,则
,则 ( )
( )
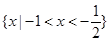


 ,且
,且
 。求
。求 的值。
的值。 =y,x
=y,x ,集合N={y︱x+y=0,x
,集合N={y︱x+y=0,x },则M
},则M N等于
N等于 0}
0} ,
,
 时,求
时,求 ;
;  ,求实数
,求实数 的取值范围.
的取值范围.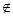 B},若A={x|0<x<2},B={x|1<x<3}则A-B等于 ( )
B},若A={x|0<x<2},B={x|1<x<3}则A-B等于 ( )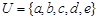 ,
,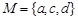 ,
,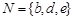 ,则
,则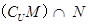 = ( )
= ( )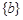
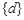
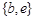
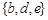
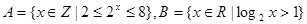 ,则
,则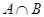 =__________.
=__________.