题目内容
已知 是关于
是关于 的一元二次方程
的一元二次方程 的两根,若
的两根,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
C.
解析试题分析:由韦达定理可得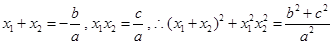 .
.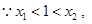
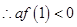 .
.
当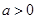 时,
时, 当
当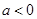 时,
时,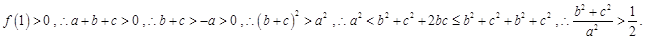
综上可得当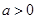 时,
时,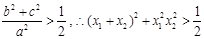 .
.
考点:应用不等式性质及重要不等式处理一元二次方程根的分布问题.

练习册系列答案
相关题目
函数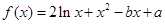
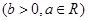 在点
在点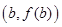 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A.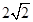 | B.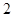 | C.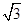 | D. |
函数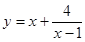
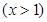 的最小值是( )
的最小值是( )
| A.3 | B.4 | C.5 | D.6 |
设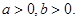 若
若 的最小值为( )
的最小值为( )
| A.8 | B.4 | C.1 | D.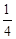 |
“a>b>0”是“ab< ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知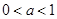 ,
,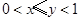 ,且
,且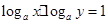 ,那么
,那么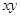 的取值范围是( )
的取值范围是( )
A.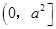 | B.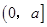 | C.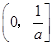 | D.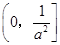 |
设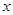 、
、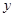 为正数,则
为正数,则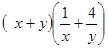 的最小值为( )
的最小值为( )
A.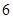 | B.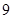 | C.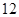 | D.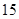 |
点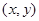 在直线
在直线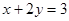 上移动,则
上移动,则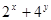 的最小值为( )
的最小值为( )
A.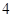 | B.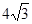 | C. | D. |
若a,b∈R,且ab>0,则下列不等式中,恒成立的是( ).
A.a+b≥2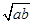 | B.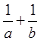 ≥ ≥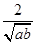 |
C.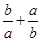 ≥2 ≥2 | D.a2+b2>2ab |