题目内容
20.两圆x2+y2-2y=0与x2+y2-4=0的位置关系是内切.分析 把圆的方程化为标准方程,求出圆心和半径,再根据两圆的圆心距正好等于半径之差,可得这2个圆的位置关系.
解答 解:圆x2+y2-2y=0,即x2+(y-1)2=1表示以点(0,1)为圆心、半径等于1的圆;
x2+y2-4=0 即 x2+y2=4,表示以点(0,0)为圆心、半径等于2的圆.
两圆的圆心距d=1,正好等于半径之差,故两圆向内切,
故答案为:内切.
点评 本题主要考查圆的标准方程,圆与圆的位置关系的判定方法,属于基础题.

练习册系列答案
相关题目
15.设a=30.3,b=50.2,c=60.1,则a,b,c的大小关系是( )
| A. | c<b<a | B. | a<c<b | C. | a<b<c | D. | c<a<b |
10.下列图象表示的函数中具有奇偶性的是( )
| A. |  | B. |  | C. |  | D. | 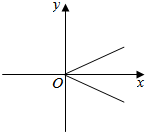 |
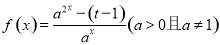 是定义域为
是定义域为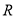 的奇函数.
的奇函数.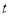 的值;
的值;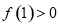 ,求使不等式
,求使不等式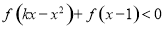 对一切
对一切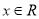 恒成立的实数
恒成立的实数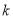 的取值范围.
的取值范围. ,若
,若 ,则实数
,则实数 的值是____________.
的值是____________.