题目内容
(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知抛物线 ,F是焦点,直线l是经过点F的任意直线.
,F是焦点,直线l是经过点F的任意直线.
(1)若直线l与抛物线交于两点A、B,且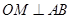 (O是坐标原点,M是垂足),求动点M的轨迹方程;
(O是坐标原点,M是垂足),求动点M的轨迹方程;
(2)若C、D两点在抛物线 上,且满足
上,且满足 ,求证直线CD必过定点,并求出定点的坐标.
,求证直线CD必过定点,并求出定点的坐标.
【答案】
所求动点M的轨迹方程是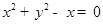 (
( ).
).
直线CD的方程可化为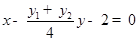 .
直线CD恒过定点,且定点坐标为(2,0).
.
直线CD恒过定点,且定点坐标为(2,0).
【解析】(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
解 (1) 设动点M的坐标为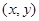 .
…………………1分
.
…………………1分
∵抛物线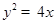 的焦点是
的焦点是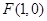 ,直线l恒过点F,且与抛物线交于两点A、B,
,直线l恒过点F,且与抛物线交于两点A、B,
又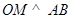 ,
,
∴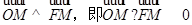 .
…………………3分
.
…………………3分
∴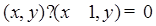 ,化简,得
,化简,得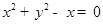 . …………………5分
. …………………5分
又当M与原点重合时,直线l与x轴重合,故 .
.
∴所求动点M的轨迹方程是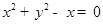 (
( ).
).
(2) 设点C、D的坐标为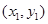 、
、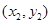 . …………………………6分
. …………………………6分
∵C、D在抛物线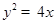 上,
上,
∴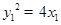 ,
,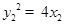 ,即
,即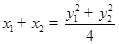 ,
,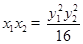 .
.
又 ,
,
∴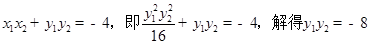 . ………8分
. ………8分
∵点C、D的坐标为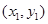 、
、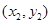 ,
,
∴直线CD的一个法向量是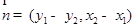 ,可得直线CD的方程为:
,可得直线CD的方程为:
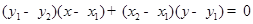 ,化简,得
,化简,得
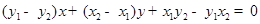 ,进一步用
,进一步用 ,有
,有
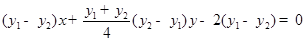 .
.
又抛物线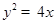 上任两点的纵坐标都不相等,即
上任两点的纵坐标都不相等,即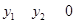 .
.
∴直线CD的方程可化为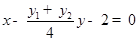 . ………………………10分
. ………………………10分
∴直线CD恒过定点,且定点坐标为(2,0). ………………………12分

练习册系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 ,
, ,…,
,…, 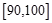 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率;
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 中, AD=2,AB=AD=4,
中, AD=2,AB=AD=4, ,点E是AB的中点,点F是
,点E是AB的中点,点F是 的中点。
的中点。  ;
;  与
与 所成的角的大小;
所成的角的大小;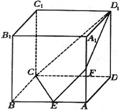
 ,且以下命题都为真命题:
,且以下命题都为真命题: 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数; 存在复数
存在复数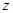 同时满足
同时满足 且
且 .
.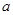 的取值范围.
的取值范围.