题目内容
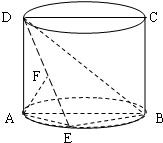 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. (Ⅰ)求证:AF⊥BD;
(Ⅱ)求二面角A-BD-E的正弦值.
分析:(Ⅰ)欲证BE⊥AF,而AF?平面ADE,可先证BE⊥平面ADE,根据直线与平面垂直的判定定理可知只需证BE与平面ADE内两相交直线垂直,根据线面垂直的性质可知BE⊥AF,又AF⊥DE,满足定理所需条件;
(Ⅱ)取BD的中点M,连接AM,FM,根据二面角平面角的定义可知∠AMF为二面角A-BD-E的平面角,过点E作EO⊥AB,垂足为O,在Rt△AFM中,求出此角的正弦值即可求出所求.
(Ⅱ)取BD的中点M,连接AM,FM,根据二面角平面角的定义可知∠AMF为二面角A-BD-E的平面角,过点E作EO⊥AB,垂足为O,在Rt△AFM中,求出此角的正弦值即可求出所求.
解答:解:(Ⅰ)因为AD⊥平面ABE,所以AD⊥BE.(1分)
又AE⊥BE,AD∩AE=A,所以BE⊥平面ADE.(2分)
因为AF?平面ADE,所以BE⊥AF.(3分)
又AF⊥DE,所以AF⊥平面BDE,故AF⊥BD.(4分)
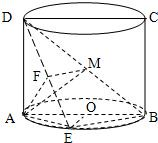 (Ⅱ)取BD的中点M,连接AM,FM.
(Ⅱ)取BD的中点M,连接AM,FM.
因为AB=AD,则AM⊥BD.因为AF⊥平面BDE,则AF⊥BD.
所以BD⊥平面AFM,从而FM⊥BD,所以∠AMF为二面角A-BD-E的平面角.(6分)
过点E作EO⊥AB,垂足为O.
设圆柱的底半径为r,因为圆柱的轴截面ABCD是正方形,
则圆柱的母线长为2r,所以其侧面积为2πr•2r=4πr2,
又△ABE的面积为
•2r•OE=r•OE.
由已知,
=4π,则OE=r,
所以点O为圆柱底面圆的圆心.(8分)
在Rt△AOE中,AE=
=
r.
在Rt△DAE中,DE=
=
r,AF=
=
=
.(10分)
又AM=ABsin45°=
r,在Rt△AFM中,sin∠AMF=
=
=
.
故二面角A-BD-E的正弦值为
.(12分)
又AE⊥BE,AD∩AE=A,所以BE⊥平面ADE.(2分)
因为AF?平面ADE,所以BE⊥AF.(3分)
又AF⊥DE,所以AF⊥平面BDE,故AF⊥BD.(4分)
 (Ⅱ)取BD的中点M,连接AM,FM.
(Ⅱ)取BD的中点M,连接AM,FM.因为AB=AD,则AM⊥BD.因为AF⊥平面BDE,则AF⊥BD.
所以BD⊥平面AFM,从而FM⊥BD,所以∠AMF为二面角A-BD-E的平面角.(6分)
过点E作EO⊥AB,垂足为O.
设圆柱的底半径为r,因为圆柱的轴截面ABCD是正方形,
则圆柱的母线长为2r,所以其侧面积为2πr•2r=4πr2,
又△ABE的面积为
| 1 |
| 2 |
由已知,
| 4πr2 |
| r•OE |
所以点O为圆柱底面圆的圆心.(8分)
在Rt△AOE中,AE=
| OA2+OE2 |
| 2 |
在Rt△DAE中,DE=
| AD2+AE2 |
| 6 |
| AD•AE |
| DE |
2
| ||
|
| 2r | ||
|
又AM=ABsin45°=
| 2 |
| AF |
| AM |
| 2 | ||||
|
| ||
| 3 |
故二面角A-BD-E的正弦值为
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的性质,以及二面角的度量等有关知识,考查空间想象能力和思维能力,计算能力,以及转化与划归的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

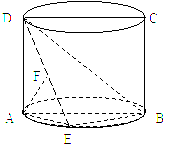 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.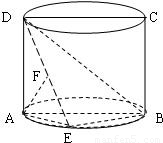
 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007