题目内容
已知
和
不共线,
=p
,
=q
(实数p≠0,q≠0),若点C在直线AB上,且
=x
+y
(x,y是实数),则
+
=
| a |
| b |
| OA |
| a |
| OB |
| b |
| OC |
| a |
| b |
| x |
| p |
| y |
| q |
1
1
.分析:利用向量的共线定理、三角形法则、向量的基本定理即可得出.
解答:解:∵点C在直线AB上,∴存在实数λ使得
=λ
,
∴
-
=λ(
-
),化为
=
+
=
+
,
又
=x
+y
(x,y是实数),
∴
,化为
+
=1.
故答案为1.
| AC |
| BC |
∴
| OC |
| OA |
| OC |
| OB |
| OC |
| 1 |
| 1-λ |
| OA |
| λ |
| 1-λ |
| OB |
| p |
| 1-λ |
| a |
| λq |
| 1-λ |
| b |
又
| OC |
| a |
| b |
∴
|
| x |
| p |
| y |
| q |
故答案为1.
点评:熟练掌握向量的共线定理、三角形法则、向量的基本定理是解题的关键.

练习册系列答案
相关题目
 ;(2)
;(2)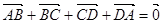 ;(3)若
;(3)若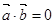 ,则
,则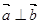 ;
; 平移后,起点和终点的发生变化,所以
平移后,起点和终点的发生变化,所以 其中正确的序号为
其中正确的序号为