题目内容
下面关于向量的结论中,
(1)|
|=|
|;
(2)
+
+
+
=
;
(3)若
•
=0,则
⊥
;
(4)若向量
平移后,起点和终点的发生变化,所以
也发生变化;
(5)已知A、B、C、D四点满足任三点不共线,但四点共面,O是平面ABCD外任一点,且
=2x•
+3y•
+4z•
,则2x+3y+4z=1.
其中正确的序号为
(1)|
| AB |
| BA |
(2)
| AB |
| BC |
| CD |
| DA |
| 0 |
(3)若
| a |
| b |
| a |
| b |
(4)若向量
| AB |
| AB |
(5)已知A、B、C、D四点满足任三点不共线,但四点共面,O是平面ABCD外任一点,且
| OA |
| OB |
| OC |
| OD |
其中正确的序号为
(1)(2)(3)(5)
(1)(2)(3)(5)
.分析:根据向量的定义,可得(1)正确而(4)不正确;根据向量的加法法则,可得(2)正确;根据向量垂直的充要条件,可得(3)正确;根据空间向量共面定理,可得(5)正确.
解答:解:根据向量的定义,可得向量
、
的大小相等且方向相反
因此有|
|=|
|成立,故(1)正确;
根据向量的加法法则,得
向量
+
+
+
=
+
+
=
+
=
,故(2)正确;
根据向量垂直的充要条件,得若
•
=0则
⊥
.故(3)正确;
根据向量的定义,向量
平移后,大小和方向都没有变化,
因此
没发生变化,故(4)不正确;
由空间向量共面定理,可得
若
=2x•
+3y•
+4z•
且A、B、C、D四点共面,则
、
、
的系数之和等于1
即2x+3y+4z=1成立,因此(5)正确.
综上所述,正确的命题为(1)(2)(3)(5)
故答案为:(1)(2)(3)(5)
| AB |
| BA |
因此有|
| AB |
| BA |
根据向量的加法法则,得
向量
| AB |
| BC |
| CD |
| DA |
| AC |
| CD |
| DA |
| AD |
| DA |
| 0 |
根据向量垂直的充要条件,得若
| a |
| b |
| a |
| b |
根据向量的定义,向量
| AB |
因此
| AB |
由空间向量共面定理,可得
若
| OA |
| OB |
| OC |
| OD |
| OB |
| OC |
| OD |
即2x+3y+4z=1成立,因此(5)正确.
综上所述,正确的命题为(1)(2)(3)(5)
故答案为:(1)(2)(3)(5)
点评:本题给出关于向量的几个命题,要求找出其中的真命题.着重考查了向量的定义、加法法则、数量积及运算性质和空间向量共面定理等知识,属于中档题.

练习册系列答案
相关题目
 ;(2)
;(2)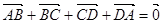 ;(3)若
;(3)若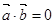 ,则
,则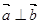 ;
; 平移后,起点和终点的发生变化,所以
平移后,起点和终点的发生变化,所以 其中正确的序号为
其中正确的序号为