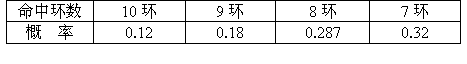题目内容
某人射击1次,命中7—10环的概率如下表所示:命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.12 | 0.18 | 0.28 | 0.32 |
(1)求射击一次,至少命中7环的概率;
(2)求射击1次,命中不足7环的概率.
解析:可根据互斥和对立事件的定义分析事件的关系,再利用互斥和对立事件的概率公式计算.
记事件“射击1次,命中k环”为 Ak(k∈N,且k≤10),则事件Ak两两相斥.
(1)记“射击一次,至少命中7环”的事件为A,那么当A10,A9,A8或A7之一发生时,事件A发生.由互斥事件的概率加法公式,得P(A)=P(A10+A9+A8+A7)=P(A10)+P(A9)+P(A8)+P(A7)=0.12+0.18+0.28+0.32=0.9.
(2)事件“射击一次,命中不足7环”是事件“射击一次,命中至少7环”的对立事件,即A表示事件“射击一次,命中不足7环”.根据对立事件的概率公式,得?P(A)=1-P(A)=1-0.9=0.1.
答:此人射击1次,至少命中7环的概率为0.9;命中不足7环的概率为0.1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目