题目内容
经过点P（0，-1）作直线l，若直线l与连接A（1，-2），B（2，1）的线段总有公共点，则直线l的倾斜角α的范围为______．
kPA=
=-1
kPB=
=1
∵l与线段AB相交，
∴kpA≤k≤kpB
∴-1≤k≤1
∴0≤tanα≤1或-1≤tanα＜0
由于y=tanx在[0，
）及（-
，0）均为减函数
∴直线l的倾斜角α的范围为：[0，
]∪[
，π)
故答案为：[0，
]∪[
，π)
| -2-(-1) |
| 1-0 |
kPB=
| 1-(-1) |
| 2-0 |
∵l与线段AB相交，
∴kpA≤k≤kpB
∴-1≤k≤1
∴0≤tanα≤1或-1≤tanα＜0
由于y=tanx在[0，
| π |
| 2 |
| π |
| 2 |
∴直线l的倾斜角α的范围为：[0，
| π |
| 4 |
| 3π |
| 4 |
故答案为：[0，
| π |
| 4 |
| 3π |
| 4 |
练习册系列答案
全能测控一本好卷系列答案
相关题目
，
，
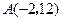三点的位置关系，并说明理由．
过点
，
，则直线
