题目内容
已知扇形的圆心角为2，半径为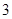
，则扇形的面积是（ ）
| A．18 | B．6 | C．3 | D．9 |
D
解析试题分析：解：根据题意，由于扇形的圆心角为2，半径为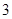，则根据扇形面积公式可知S=
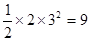，故选D.
考点：扇形的面积
点评:本题考查扇形的面积公式的应用，求出扇形的圆心角的弧度数是解题的突破口
练习册系列答案
阅读快车系列答案
相关题目
函数
（其中A＞0，
）的图象如图所示，为了得到
的图象，则只需将g(x)=sin2x的图象
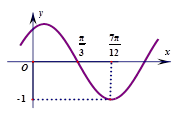
A．向右平移 个长度单位 |
| B．向左平移个长度单位 |
C．向右平移 个长度单位 |
| D．向左平移个长度单位 |
函数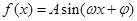
(其中A>0, 
)的图象如图所示，为了得到g(x =cos2x的图象,则只需将f(x)的图象
A．向右平移 个单位长度 | B．向右平移 个单位长度 |
| C．向左平移个单位长度 | D．向左平移个单位长度 |
的图象向左平移
个单位，再把所得函数图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），得到图象的解析式为（ ）
已知点
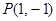落在角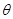
的终边上，则
的值为（ ）
A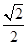． | B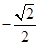． | C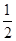． | D． |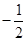
要得到函数
的图像，只需要将函数
的图像（ ）
A．向左平移 个单位 | B．向右平移个单位 |
C．向左平移 个单位 | D．向右平移个单位 |
函数
的相邻两条对称轴之间的距离为 ( )
A． | B． | C． | D． |
若将函数
的图象向右平移
个单位长度后与函数
的图象重合，则
的最小值为（ ）
| A．1 | B．2 | C． | D． |
已知奇函数f（x）在[－1，0]上为单调递减函数，又a，b为锐角三角形两内角，下列结论正确的是
| A．f（cosa）> f（cosb） | B．f（sina）> f（sinb） |
| C．f（sina）> f（cosb） | D．f（sina）<f（cosb） |