题目内容
已知R上的函数y=f（x），其周期为2，且x∈（-1,1]时f（x）=1+x2，函数g（x）=
，则函数h（x）=f（x）－g（x）在区间[-5,5]上的零点的个数为（ ）
A．11 B．10 C．9 D．8
【答案】
C
【解析】
试题分析：易知，当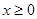
时零点分别是，0,1,2,4,5共5个，当
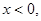函数在区间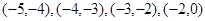
间分别有一个零点，故共9个零点.
考点：函数的零点
点评：解决本题的关键是把函数有零点的问题，转化成两函数在某区间内有交点的问题，属中档题.
练习册系列答案
相关题目
定义在R上的函数y=f（x）满足f（5+x）=f（-x），（x-
）f′（x）＞0，已知x1＜x2，则f（x1）＞f（x2）是x1+x2＜5的（ ）条件．
| 5 |
| 2 |
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
，则函数h（x）=f（x）-g（x）在区间[-5,5]上的零点的个数为