Question

（2009安徽卷文）（本小题满分12分）

已知椭圆（a＞b＞0）的离心率为，以原点为圆心。椭圆短半轴长半径的

圆与直线y=x+2相切，

（Ⅰ）求a与b；21世纪教育网      

（Ⅱ）设该椭圆的左，右焦点分别为和，直线过且与x轴垂直，动直线与y轴垂直，交与点p..求线段P垂直平分线与的交点M的轨迹方程，并指明曲线类型。

Answer 1

【思路】（1）由椭圆建立a、b等量关系，再根据直线与椭圆相切求出a、b.

（2）依据几何关系转化为代数方程可求得，这之中的消参就很重要了。

【解析】（1）由于  ∴  ∴  又  ∴b²=2,a²=3因此，. 21世纪教育网      

（2）由（1）知F₁，F₂两点分别为（-1，0），（1,0），由题意可设P（1，t）.（t≠0）.那么线段PF₁中点为，设M(x、y)是所求轨迹上的任意点.由于则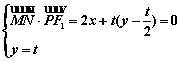消去参数t得

,其轨迹为抛物线（除原点）