题目内容
已知f(x)=|x+4|-|x-6|的最大值为n,则二项式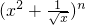 展开式中常数项等于
展开式中常数项等于
- A.21
- B.28
- C.36
- D.45
D
分析:根据绝对值的意义求得f(x)=|x+4|-|x-6|的最大值n=10,在二项式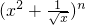 展开式通项公式中,令x的系数等于0,
展开式通项公式中,令x的系数等于0,
求出 r=8,从而求得展开式中的常数项.
解答:由于f(x)=|x+4|-|x-6|表示数轴上的x对应点到-4对应点的距离减去它到6对应点的距离,
最大值为10,故n=10.
则二项式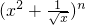 展开式通项为 Tr+1=
展开式通项为 Tr+1= (x2)n-r
(x2)n-r 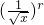 =
=
 ,
,
令20-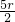 =0,r=8,
=0,r=8,
故展开式中常数项等于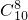 =45,
=45,
故选D.
点评:本题主要考查绝对值的意义,二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.
分析:根据绝对值的意义求得f(x)=|x+4|-|x-6|的最大值n=10,在二项式
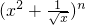 展开式通项公式中,令x的系数等于0,
展开式通项公式中,令x的系数等于0,求出 r=8,从而求得展开式中的常数项.
解答:由于f(x)=|x+4|-|x-6|表示数轴上的x对应点到-4对应点的距离减去它到6对应点的距离,
最大值为10,故n=10.
则二项式
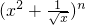 展开式通项为 Tr+1=
展开式通项为 Tr+1= (x2)n-r
(x2)n-r 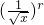 =
=
 ,
,令20-
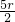 =0,r=8,
=0,r=8,故展开式中常数项等于
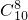 =45,
=45,故选D.
点评:本题主要考查绝对值的意义,二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.