题目内容
已知定义在R上的函数 满足:对任意x∈R,都有
满足:对任意x∈R,都有 成立,且当
成立,且当 时,
时, (其中
(其中 为
为 的导数).设
的导数).设 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )
A. | B. | C. | D. |
B
解析试题分析:由题意得:对任意x∈R,都有 ,即f(x)=f(2-x)成立,
,即f(x)=f(2-x)成立,
所以函数的对称轴为x=1,所以f(3)=f(-1).
因为当x∈(-∞,1)时,(x-1)f′(x)<0,
所以f′(x)>0,所以函数f(x)在(-∞,1)上单调递增.
因为-1<0<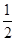 ,所以f(-1)<f(0)<f(
,所以f(-1)<f(0)<f(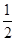 ),即f(3)<f(0)<f(
),即f(3)<f(0)<f(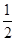 ),所以c<a<b.
),所以c<a<b.
故选B.
考点:本题主要考查熟练函数的奇偶性、单调性、对称性等,利用导数研究函数的单调性。
点评:中档题,熟练掌握函数的性质如奇偶性、单调性、周期性、对称性等,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。自左向右看,函数图象上升,函数增;函数图象下降,函数减。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
夏季高山上温度从山脚起每升高100米,降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则山的相对高度是( ) 米.
| A.1800 | B.1700 | C.1600 | D.1500 |
函数 的单调递增区间为( )
的单调递增区间为( )
A. | B. | C. | D. |
设函数 ,且
,且 恒成立,则对
恒成立,则对 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )
A. | B. | C. | D. |
设 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
若 且
且 ,在定义域
,在定义域 上满足
上满足 ,则
,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.[ ,1) ,1) | C.(0, ] ] | D.(0,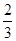 ] ] |
已知函数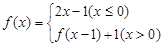 ,把函数
,把函数 的零点按从小到大的顺序排列成一个数列,该数列的前
的零点按从小到大的顺序排列成一个数列,该数列的前 项的和
项的和 ,则
,则 = ( )
= ( )
| A.45 | B.55 | C. | D. |
设函数 若
若 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
函数 在区间
在区间 上单调递减,那么实数
上单调递减,那么实数 的取值范围是( )
的取值范围是( )
A. ≤-2 ≤-2 | B. ≥-2 ≥-2 | C. ≤4 ≤4 | D. ≥4 ≥4 |