题目内容
(Ⅰ)已知函数f(x)=x3-x,其图象记为曲线C,
(ⅰ)求函数f(x)的单调区间;
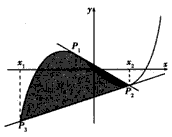
(ⅱ)证明:若对于任意非零实数x1,曲线C与其在点P1(x1,f(x1))处的切线交于另一点P2(x2,f(x2)),曲线C与其在点P2处的切线交于另一点P3(x3,f(x3)),线段P1P2,P2P3与曲线C所围成封闭图形的面积分别记为S1,S2,则 为定值;
为定值;
(Ⅱ)对于一般的三次函数g(x)=ax3+bx2+cx+d(a≠0),请给出类似于(Ⅰ)(ⅱ)的正确命题,并予以证明.
(ⅰ)求函数f(x)的单调区间;
(ⅱ)证明:若对于任意非零实数x1,曲线C与其在点P1(x1,f(x1))处的切线交于另一点P2(x2,f(x2)),曲线C与其在点P2处的切线交于另一点P3(x3,f(x3)),线段P1P2,P2P3与曲线C所围成封闭图形的面积分别记为S1,S2,则
 为定值;
为定值;(Ⅱ)对于一般的三次函数g(x)=ax3+bx2+cx+d(a≠0),请给出类似于(Ⅰ)(ⅱ)的正确命题,并予以证明.
|
解:(Ⅰ)(ⅰ)由f(x)=x3-x得f′(x)=3x2-1= |
 |
| (Ⅱ)记函数g(x)=ax3+bx2+cx+d(a≠0)的图象为曲线C′, 类似于(Ⅰ)(ⅱ)的正确命题为:若对于任意不等于 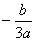 的实数x1,曲线C′与其在点P1(x1,g(x1))处的切线交于另一点P2(x2,g(x2)),曲线C′与其在点P2处的切线交于另一点P3(x3,g(x3)),线段P1P2,P2P3与曲线C′所围成封闭图形的面积分别别为S1,S2,则 的实数x1,曲线C′与其在点P1(x1,g(x1))处的切线交于另一点P2(x2,g(x2)),曲线C′与其在点P2处的切线交于另一点P3(x3,g(x3)),线段P1P2,P2P3与曲线C′所围成封闭图形的面积分别别为S1,S2,则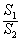 为定值. 为定值.证明如下:因为平移变换不改变面积的大小, 故可将曲线y=g(x)的对称中心 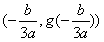 平移至坐标原点, 平移至坐标原点,因而不妨设g(x)=ax3+hx,且x1≠0, 类似(Ⅰ)(ⅱ)的计算可得 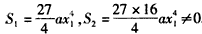 , ,故 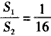 。 。 |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
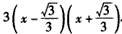 ,
,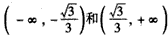 时,f′(x)>0;
时,f′(x)>0;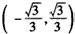 时,f′(x)<0;
时,f′(x)<0; ,
,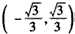 。
。 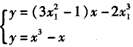 得x3-x=(3x12-1)x-2x13,
得x3-x=(3x12-1)x-2x13,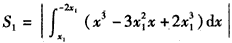
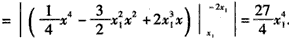 ,
,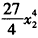 ;
; ,
,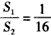 。
。