题目内容
（不等式选讲）如果关于x的不等式|x+1|+|x-3|＜a的解集不是空集，则实数a的取值范围是
a＞4
a＞4
．分析：先求不等式|x+1|+|x-3|的最大值，要求解集不是空集时实数a的取值范围，只要a大于不等式|x+1|+|x-3|的最小值即可．
解答：解：|x+1|+|x-3|的几何意义是数轴上的点x 到-1和3的距离之和，
当x在3、-1之间时，这个距离和最小，最小值是4．其它情况都大于4，
所以|x+1|+|x-3|≥4，
如果不是空集，所以 a＞4．
故答案为：a＞4．
当x在3、-1之间时，这个距离和最小，最小值是4．其它情况都大于4，
所以|x+1|+|x-3|≥4，
如果不是空集，所以 a＞4．
故答案为：a＞4．
点评：本题考查绝对值不等式的几何意义，是基础题．表示出原不等式左边的最小值是解本题的关键．
练习册系列答案
相关题目
和
的两个圆的圆心距为 ；
的解集不是空集，则实数
的取值范围是 ；
，且AE=2，则AC= ； 
和
的两个圆的圆心距为
； 
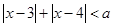的解集不是空集，则实数a的取值范围是 ； 
，且AE=2，则AC= ． 
的解集不是空集，则实数a的取值范围是
。